Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,B\) trên mặt đất sao cho ba điểm \(A,\,B,\,C\) thẳng hàng. Ta đo được \(AB = 24m\) \(\widehat {CAD} = 63^\circ \); \(\widehat {CBD} = 48^\circ \). Chiều cao \(h\) của khối tháp gần với giá trị nào sau đây?
Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: A
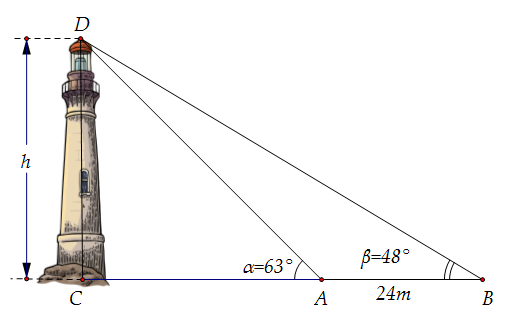
Ta có \(\widehat {CAD} = 63^\circ \Rightarrow \widehat {BAD} = 117^\circ \Rightarrow \widehat {ADB} = 180^\circ - \left( {117^\circ + 48^\circ } \right) = 15^\circ \)
Áp dụng định lý sin trong tam giác \(ABD\) ta có:
\(\frac{{AB}}{{\sin \widehat {ADB}}} = \frac{{BD}}{{\sin \widehat {BAD}}} \Rightarrow BD = \frac{{AB.\sin \widehat {BAD}}}{{\sin \widehat {ADB}}}\)
Tam giác \(BCD\) vuông tại \(C\) nên có: \(\sin \widehat {CBD} = \frac{{CD}}{{BD}} \Rightarrow CD = BD.\sin \widehat {CBD}\)
Vậy \[CD = \frac{{AB.\sin \widehat {BAD}.\sin \widehat {CBD}}}{{\sin \widehat {ADB}}} = \frac{{24.\sin 117^\circ .sin48^\circ }}{{\sin 15^\circ }} = 61,4m\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x,\,y\) lần lượt là số radio kiểu một và kiểu hai sản xuất được trong một ngày. \(\left( {x,\,\,y \ge 0} \right)\)
Vì radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày nên \(x \le 45,\,\,y \le 80\).
Sản xuất \(x\) chiếc radio kiểu một và \(y\) chiếc radio kiểu hai cần số linh kiện là \(12x + 9y\).
Mà số linh kiện có thể sử dụng tối đa trong một ngày là 900 nên \(12x + 9y \le 900\) hay tương đương với \(4x + 3y \le 300\).
Tiền lãi thu được khi bán \(x\) chiếc radio kiểu một và \(y\) chiếc radio kiểu hai là \(T = 250\,\,000x + 180\,\,000y\) (đồng).
Khi đó, bài toán đã cho trở thành: Tìm \(\left( {x;\,\,y} \right)\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\4x + 3y \le 300\end{array} \right.\)để \(T = 250\,\,000x + 180\,\,000y\) lớn nhất.
Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\4x + 3y \le 300\end{array} \right.\) lên mặt phẳng tọa độ \(Oxy\) ta được:
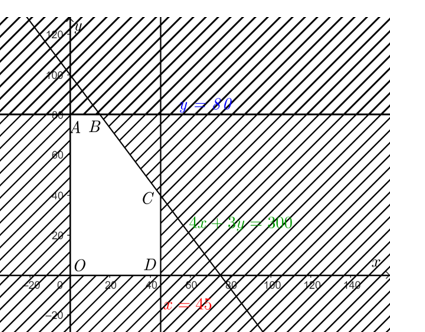
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}0 \le x \le 45\\0 \le y \le 80\\4x + 3y \le 300\end{array} \right.\) là miền ngũ giác \(OABCD\) (kể cả biên) với \(O\left( {0;\,\,0} \right),\,\,A\left( {0;\,\,80} \right),\,\,B\left( {15;\,\,80} \right),\,\,C\left( {45;\,\,40} \right),\,\,D\left( {45;\,\,0} \right)\).
Người ta chứng minh được \(T = 250\,\,000x + 180\,\,000y\) đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác \(OABCD\).
Ta có: \(T\left( {0;\,\,0} \right) = 0\);
\(T\left( {0;\,\,80} \right) = 250\,\,000 \cdot 0 + 180\,\,000 \cdot 80 = 14\,\,400\,\,000\);
\(T\left( {15;\,\,80} \right) = 250\,\,000 \cdot 15 + 180\,\,000 \cdot 80 = 18\,\,150\,\,000\);
\(T\left( {45;\,\,40} \right) = 250\,\,000 \cdot 45 + 180\,\,000 \cdot 40 = 18\,\,450\,\,000\);
\(T\left( {45;\,\,0} \right) = 250\,\,000 \cdot 45 + 180\,\,000 \cdot 0 = 11\,\,250\,\,000\).
Do đó, \(T = 250\,\,000x + 180\,\,000y\) đạt giá trị lớn nhất tại \(\left( {x;\,\,y} \right) = \left( {45;\,\,40} \right)\).
Vậy cần sản xuất 45 radio kiểu một và 40 radio kiểu hai thì lãi thu được trong một ngày là lớn nhất.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Diện tích tam giác \[ABC\] đều là:
\[S = AB.AC.sinA = \frac{1}{2}.2a.2a.sin60^\circ = {a^2}\sqrt 3 \]
Nửa chu vi tam giác \[ABC\] là:
\[p = \frac{{2a + 2a + 2a}}{2} = 3a\]
Bán kính đường tròn nội tiếp tam giác \[ABC\] là:
\[r = \frac{S}{p} = \frac{{{a^2}\sqrt 3 }}{{3a}} = \frac{a}{{\sqrt 3 }}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.