Cho hai biến cố A, B với P(B) = 0,6; . Khi đó \(P\left( {AB} \right)\) bằng\(P\left( {A|B} \right) = 0,5\)

Toàn thể nhân viên của một công ty được hỏi ý kiến về một dự thảo chính sách phúc lợi mới. Kết quả được ghi lại ở bảng sau

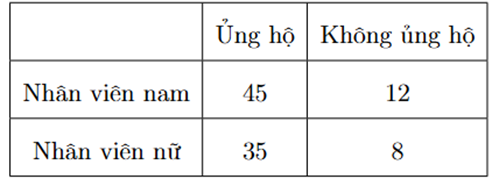
Chọn ngẫu nhiên một nhân viên của công ty. Gọi A là biến cố “Nhân viên đó là nam giới”, B là biến cố “Nhân viên đó ủng hộ dự thảo chính sách phúc lợi mới”.

Xác suất của biến cố A với điều kiện B là

Gọi A là biến cố “Lấy được viên bi xanh ở lần thứ nhất”;

B là biến cố “Lấy được viên bi trắng ở lần thứ hai”.

Ta có \(P\left( A \right) = \frac{{30}}{{50}} = \frac{3}{5};P\left( {B|A} \right) = \frac{{20}}{{49}}\).

Khi đó \(P\left( {AB} \right) = P\left( A \right).P\left( {B|A} \right) = \frac{3}{5}.\frac{{20}}{{49}} = \frac{{12}}{{49}} \approx 0,24\).

Trả lời: 0,24.

Gọi A là biến cố “Sản phẩm lấy ra lần thứ hai bị lỗi”;

B là biến cố “Sản phẩm lấy ra lần thứ nhất bị lỗi”.

Ta có \(P\left( B \right) = \frac{{39}}{{2000}} \Rightarrow P\left( B \right) = \frac{{1961}}{{2000}}\). \(P\left( {A|B} \right) = \frac{{38}}{{1999}};P\left( {A|\overline B } \right) = \frac{{39}}{{1999}}\).

Khi đó \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\)\( = \frac{{39}}{{2000}}.\frac{{38}}{{1999}} + \frac{{1961}}{{2000}}.\frac{{39}}{{1999}} \approx 0,02\).

Trả lời: 0,02.