Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{x}{{\sqrt {x + 1} }}\) là

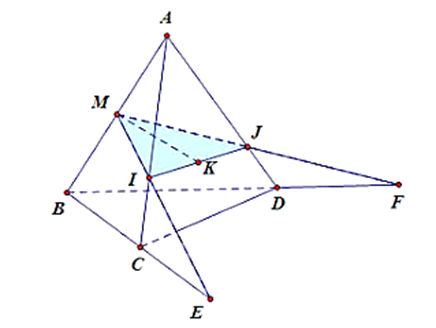
a) +) Trong mặt phẳng \(\left( {ABC} \right)\) có \(ME \cap AC = I\)

Mà \(AC \subset \left( {ABC} \right),ME \subset \left( {MEF} \right)\) nên \(I \in \left( {ABC} \right) \cap \left( {MEF} \right)\)

Lại có \(M \in \left( {ABC} \right) \cap \left( {MEF} \right)\)

Nên \(MI = \left( {ABC} \right) \cap \left( {MEF} \right)\).

+) Trong mặt phẳng \(\left( {ABD} \right)\) có \(MF \cap AD = J\)

Mà \(AD \subset \left( {ABD} \right),MF \subset \left( {MEF} \right)\) nên \(J \in \left( {ABD} \right) \cap \left( {MEF} \right)\)

Lại có \(M \in \left( {ABD} \right) \cap \left( {MEF} \right)\)

Nên \(MJ = \left( {ABD} \right) \cap \left( {MEF} \right)\).

Tương tự, ta có \(IJ = \left( {ACD} \right) \cap \left( {MEF} \right)\).

Do đó thiết diện của tứ diện với mặt phẳng \(\left( {MEF} \right)\) là \(\Delta MIJ\).

b) Vì \(I,J\) lần lượt là trọng tâm \(\Delta ABE,\Delta ABF\) nên \(\left\{ \begin{array}{l}AI = \frac{2}{3}AC = \frac{2}{3}a\\AJ = \frac{2}{3}AD = \frac{2}{3}a\end{array} \right.\).

Vì \(ABCD\) là tứ diện đều nên \(\Delta ACD\) đều, suy ra \(\widehat {CAD} = \widehat {IAJ} = 60^\circ \).

Vì \(\widehat {IAJ} = 60^\circ \) và \(AI = AJ\) nên \(\Delta AIJ\) đều, suy ra \(IJ = \frac{2}{3}a\).

Do \(M\)là trung điểm của \(AB\) nên \(AM = \frac{{AB}}{2} = \frac{a}{2}\).

Xét \(\Delta AMJ\) có \(\widehat {MAJ} = 60^\circ \), ta có:

\(MJ = \sqrt {A{M^2} + A{J^2} - 2AM \cdot AJ \cdot \cos \widehat {MAJ}} \)

\(MJ = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{2a}}{3}} \right)}^2} - 2 \cdot \frac{a}{2} \cdot \frac{{2a}}{3} \cdot \cos 60^\circ } \)\( = \frac{{a\sqrt {13} }}{6}\)

Xét \(\Delta AMI\) có \(\widehat {MAI} = 60^\circ \), ta có:

\(MI = \sqrt {A{M^2} + A{I^2} - 2AM \cdot AI \cdot \cos \widehat {MAI}} \)

\(MI = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{2a}}{3}} \right)}^2} - 2 \cdot \frac{a}{2} \cdot \frac{{2a}}{3} \cdot \cos 60^\circ } \)\( = \frac{{a\sqrt {13} }}{6}\).

Do \(MI = MJ = \frac{{a\sqrt {13} }}{6}\) nên \(\Delta MIJ\) cân tại \(M\).

Gọi \(K\) là trung điểm của \(IJ\). Suy ra \(IK = KJ = \frac{{IJ}}{2} = \frac{a}{3}\).

Vì \(\Delta MIJ\) cân có \(MK\) là trung tuyến nên \(MK\) đồng thời là đường cao.

Xét \(\Delta MKI\) có \(MK = \sqrt {M{I^2} - I{K^2}} = \sqrt {{{\frac{{13a}}{{36}}}^2} - \frac{{{a^2}}}{9}} = \frac{a}{2}\).

Khi đó \({S_{MIJ}} = \frac{1}{2}MK \cdot IJ = \frac{1}{2} \cdot \frac{a}{2} \cdot \frac{{2a}}{3} = \frac{{{a^2}}}{6}.\)

Đáp án đúng là: C

Cỡ mẫu \(n = 5 + 2 + 3 + 1 = 11.\)

Gọi \({x_1},...,{x_{11}}\) là số huy chương mà 11 quốc gia đạt được giả sử dãy này đã được sắp xếp theo thứ tự không giảm.

Khi đó: \({x_1},...,{x_5}\) thuộc nhóm \[\left[ {0;10} \right)\];

\({x_6};{x_7}\) thuộc nhóm \(\left[ {10;50} \right)\);

\({x_8},...,{x_{10}}\) thuộc nhóm \(\left[ {50;100} \right)\);

\({x_{11}}\) thuộc nhóm \(\left[ {100;210} \right)\).

Ta có trung vị thuộc nhóm \(\left[ {10;50} \right)\).

Do đó, \(n = 11;{n_m} = 2;C = 5;{u_m} = 10;{u_{m + 1}} = 50\).

Vậy trung vị của mẫu số liệu ghép nhóm là

\({M_e} = 10 + \frac{{\frac{{11}}{2} - 5}}{2}.\left( {50 - 10} \right) = 20\).