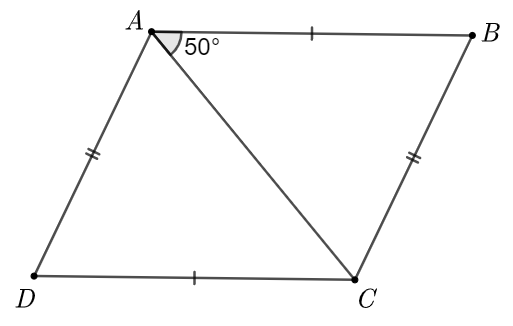
Cho tứ giác \(ABCD\) có \(AB = CD\); \(AD = BC\) (như hình vẽ). Biết \(\widehat {BAC} = 50^\circ \), số đo của \[\widehat {ACD}\] là

Sau đợt thứ nhất, bác Minh lãi số tiền là:

\(30\,\,.\,\,\left( {9,8 - 8} \right) = 54\) (triệu đồng).

Sau đợt thứ hai, bác Minh lãi số tiền là:

\(10\,\,.\,\,\left( {9,5 - 8} \right) = 15\) (triệu đồng).

Để lợi nhuận đạt tỉ lệ 20% thì số tiền lãi bác Minh thu được là:

\(50\,\,.\,\,8\,\,.\,\,20\% = 80\) (triệu đồng).

Số chiếc điện thoại còn lại sau hai đợt bán là:

\(50 - 30 - 10 = 10\) (chiếc điện thoại).

Số tiền lãi cần đạt được khi bán 10 chiếc điện thoại còn lại là:

\[80 - 54 - 15 = 11\] (triệu đồng).

Với 10 chiếc điện thoại có giá 11 triệu đồng thì giá tiền mỗi chiếc điện thoại là:

\(11\,\,:\,\,10 = 1,1\) (triệu đồng).

Vậy bác Minh phải bán mỗi chiếc điện thoại còn lại với giá 1,1 triệu đồng để lợi nhuận đạt tỉ lệ 20%.

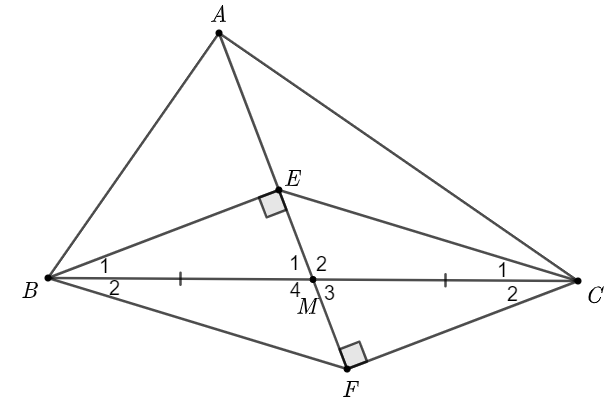
a) Theo giả thiết: \(BE \bot Ax\), \(CF \bot Ax\)

Suy ra \(BE\parallel CF\).

b) So sánh \(BE\) và \(FC\); \(CE\) và \(BF\).

• Xét \(\Delta MBE\) và \(\Delta MCF\) có:

\({\widehat B_1} = {\widehat C_2}\) (hai góc so le trong);

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\({\widehat M_1} = {\widehat M_3}\) (hai góc đối đỉnh).

Do đó \(\Delta MBE = \Delta MCF\) (g.c.g)

Suy ra \(BE = CF\) (hai cạnh tương ứng).

• Xét \(\Delta MBF\) và \(\Delta MCE\) có:

\({\widehat B_2} = {\widehat C_1}\) (hai góc so le trong);

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\({\widehat M_2} = {\widehat M_4}\) (hai góc đối đỉnh).

Do đó \(\Delta MBF = \Delta MCE\) (g.c.g)

Suy ra \(BF = CE\) (hai cạnh tương ứng).

Vậy \(BE = CF\); \(BF = CE\).

c) Xét \(\Delta BEM\) và \(\Delta CEM\) có:

\(BE = CE\) (giả thiết);

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\(EM\) là cạnh chung

Do đó \(\Delta BEM = \Delta CEM\) (c.c.c).

d) Từ câu c: \(\Delta BEM = \Delta CEM\)

Suy ra \(\widehat {BME} = \widehat {CME}\) (hai góc tương ứng).

Mặt khác, \(\widehat {BME} + \widehat {CME} = 180^\circ \) (hai góc kề bù) nên \(\widehat {BME} = \widehat {CME} = 90^\circ \).

Suy ra \(EM \bot BC\) hay \(AM \bot BC\).

Xét \(\Delta BAM\) và \(\Delta CAM\) có:

\(BM = CM\) (vì \(M\) là trung điểm của \(BC\));

\(\widehat {BAM} = \widehat {CAM} = 90^\circ \);

\(AM\) là cạnh chung

Do đó \(\Delta BAM = \Delta CAM\) (c.g.c).

Suy ra \(AB = AC\) (hai cạnh tương ứng).

Do đó tam giác \(ABC\) cân tại \(A\).

Vậy tam giác \(ABC\) cân tại \(A\) thì \(BE = CE\).