khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 7
  3. Toán

Câu hỏi:

22/11/2025 248 Lưu

(1,0 điểm) Cho biểu đồ dưới đây:

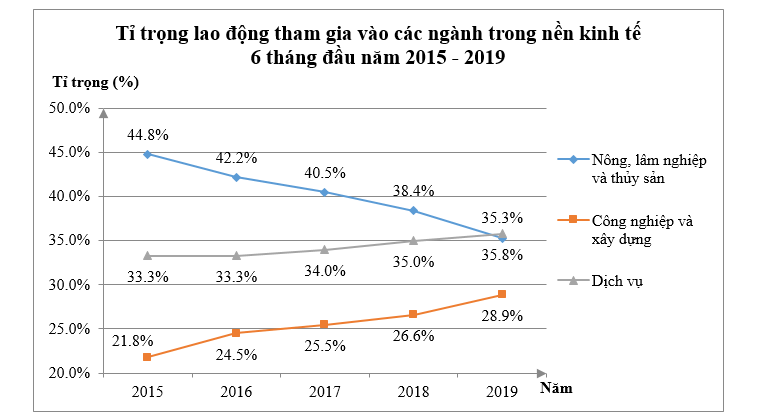
 (1,0 điểm) Cho biểu đồ dưới đây: Quan sát biểu đồ trên và trả lời các câu hỏi sau: a) Vào năm 2017, ngành nào có tỉ trọng lao động thấp nhất trong cả ba ngành? (ảnh 1)

Quan sát biểu đồ trên và trả lời các câu hỏi sau:

a) Vào năm 2017, ngành nào có tỉ trọng lao động thấp nhất trong cả ba ngành?

b) Phân tích xu thế về tỉ trọng lao động tham gia vào mỗi ngành trong 6 tháng đầu năm giai đoạn 2015 – 2019.

Xem lời giải

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Kết nối tri thức có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Vào năm 2017, ngành công nghiệp và xây dựng có tỉ trọng lao động thấp nhất trong cả ba ngành.

b) Ngành công nghiệp và xây dựng; ngành dịch vụ: tỉ trọng lao động tham gia có xu hướng tăng.

Ngành ngành nông, lâm nghiệp và thủy sản: tỉ trọng lao động tham gia có xu hướng giảm.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

(2,5 điểm) Cho \(\Delta ABC\) cân tại \(A\). Gọi \(AD\) là tia phân giác của \(\widehat {BAC}\) (\(D \in BC\)). Kẻ \(DE \bot AB\) tại \(E\), \(DF \bot AC\) tại \(F\).

a) Chứng minh \(\Delta ABD = \Delta ACD\).

b) Chứng minh \(DE = DF\).

c) Chứng minh \(EF\,{\rm{//}}\,BC\).

Lời giải

Cho \(\Delta ABC\) cân tại \(A\). Gọi \(AD\) là (ảnh 1)

a) Xét \(\Delta ABD\) và \(\Delta ACD\), có:

\(AB = AC\) (do \(\Delta ABC\) cân tại \(A\));

\(\widehat {BAD} = \widehat {CAD}\) (do \(AD\) là tia phân giác của \(\widehat {BAC}\));

\(AD\) là cạnh chung.

Do đó \(\Delta ABD = \Delta ACD\) (c.g.c)

b) Xét \(\Delta ADE\) và \(\Delta ADF\), có:

\[\widehat {AED} = \widehat {AFD} = 90^\circ \];

\(AD\) là cạnh chung;

\(\widehat {EAD} = \widehat {FAD}\) (do \(AD\) là tia phân giác của \(\widehat {BAC}\)).

Do đó \(\Delta ADE = \Delta ADF\) (cạnh huyền – góc nhọn)

Suy ra \(DE = DF\) (cặp cạnh tương ứng).

c) Ta có \(AE = AF\) (Do \(\Delta ADE = \Delta ADF\))

Suy ra \(\Delta AEF\) cân tại \(A\) nên \[\widehat {AEF} = \widehat {AFE}\].

Mà \(\widehat {EAF} + \widehat {AEF} + \widehat {AFE} = 180^\circ \) (định lí tổng ba góc trong một tam giác)

Suy ra \(\widehat {AEF} = \frac{{180^\circ - \widehat {EAF}}}{2} = \frac{{180^\circ - \widehat {BAC}}}{2}\).

Chứng minh tương tự đối với \[\Delta ABC\] cân tại A, ta được \(\widehat {ABC} = \frac{{180^\circ - \widehat {BAC}}}{2}\).

Khi đó \(\widehat {AEF} = \widehat {ABC}\).

Mà hai góc này ở vị trí đồng vị nên \(EF\,{\rm{//}}\,BC\).

Câu 2

(0,5 điểm) Một nền nhà hình chữ nhật có chiều dài 12 m và chiều rộng 5 m. Người ta dự định lát các các viên gạch hình vuông có cạnh 30 cm. Coi các mạch ghép là không đáng kể, người ta cần mua ít nhất bao nhiêu viên gạch biết khi đến cửa hàng bán gạch lát thì cửa hàng nói rằng chỉ bán theo viên?

Lời giải

Diện tích nền nhà là: 12 . 5 = 60 (m2).

Đổi: 30 cm = 0,3 m.

Diện tích một viên gạch là: \(0,{3^2} = 0,09\) (m2).

Số viên gạch cần dùng là: 60 : 0,09 = 666,666… (viên gạch).

Vậy người ta cần mua 666 + 1 = 667 viên gạch.

Câu 3

(0,5 điểm) Một công ty phát triển kĩ thuật cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 24 ngày. Nhóm kĩ thuật viên được nhận làm dự án sẽ được trả tiền công như sau: ngày đầu tiên nhận 4 triệu đồng, ngày sau tăng thêm 5% tiền công ngày trước đó. Tính số tiền công mà nhóm kĩ thuật đó nhận được sau khi hoàn thành dự án.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Phân số nào sau đây không viết được dưới dạng số thập phân hữu hạn?        
A. \[\frac{3}{{21}}\];                              
B. \(\frac{3}{{12}}\);           
C. \(\frac{3}{{25}}\);           
D. \(\frac{7}{{35}}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Kết quả làm tròn số \[0,7125\] với độ chính xác \[0,0005\] là:        
A. \[0,700\];             
B. \[0,713\];             
C. \[0,712\];                          
D. \[0,710\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

PHẦN II. TỰ LUẬN (7,0 điểm)

(1,5 điểm) Thực hiện phép tính (tính hợp lí nếu có thể):

a) \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\);                  

b) \(5\frac{6}{7}.\left( { - \frac{5}{6} + \frac{1}{7}} \right) + \frac{{41}}{7}.\left( { - \frac{1}{6} + \frac{6}{7}} \right)\);     

c) \({2^2}.\sqrt {16} - {\left( {\sqrt 7 } \right)^2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Biểu đồ sau đây cho biết tỉ lệ các loại bút một cửa hàng bán được trong một ngày:

 Biểu đồ sau đây cho biết tỉ lệ các loại bút một cửa hàng bán được trong một ngày: (ảnh 1)

Phát biểu nào sau đây sai?
A. Hình tròn trên được chia thành 4 hình quạt;
B. Số lượng bút bi xanh bán được chiếm \[40\% \];
C. Số lượng bút chì bán được chiếm \[25\% \];
D. Số lượng bút dạ quang bán được chiếm \(5\% \).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập