(1,0 điểm) Một lăng kính thủy tinh có dạng hình lăng trụ đứng có đáy là tam giác đều, kích thước như bình bên.
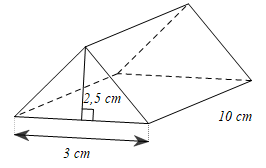
a) Tính thể tích của lăng kính thủy tinh đó.
b) Người ta làm một chiếc hộp bằng bìa cứng để đựng vừa khít lăng kính thủy tinh nói trên (hở hai đáy tam giác). Tính diện tích bìa cần dùng (bỏ qua mép nối).
(1,0 điểm) Một lăng kính thủy tinh có dạng hình lăng trụ đứng có đáy là tam giác đều, kích thước như bình bên.

a) Tính thể tích của lăng kính thủy tinh đó.
b) Người ta làm một chiếc hộp bằng bìa cứng để đựng vừa khít lăng kính thủy tinh nói trên (hở hai đáy tam giác). Tính diện tích bìa cần dùng (bỏ qua mép nối).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Diện tích đáy tam giác của lăng trụ là .
Thể tích của lăng trụ đó là: .
b) Chu vi đáy tam giác của lăng trụ là: .
Diện tích bìa cần dùng là: \(S = 9.10 = 90\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
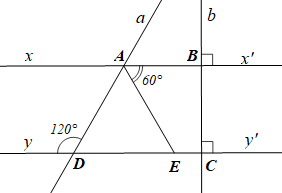
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(a,\,b,\,xx',\,yy'\) là các đường thẳng; \(a\) cắt \(xx'\) tại \(A\), \(a\) cắt \(yy'\) tại \(D\), \(\widehat {ADy} = 120^\circ \); \(b \bot xx'\) tại \(B\), \(b \bot yy'\) tại \(C\), \(\widehat {BAE} = 60^\circ \). |
|
KL |
b) \[xx'{\rm{ // }}yy'\]. c) Tìm \(\widehat {BAD}\). d) Tia \[AE\] là tia phân giác của \(\widehat {BAD}\) |
b) Do \(b \bot xx'\) và \(b \bot yy'\) nên \[xx'{\rm{ // }}yy'\] (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau).
c) Do \[xx'{\rm{ // }}yy'\] (câu a) nên \(\widehat {BAD} = \widehat {ADy}\) (hai góc so le trong)
Mà \(\widehat {ADy} = 120^\circ \) (giả thiết) nên \[\widehat {BAD} = 120^\circ \].
d) Ta có \(\widehat {BAE} + \widehat {DAE} = \widehat {BAD}\) (hai góc kề nhau)
\(60^\circ + \widehat {DAE} = 120^\circ \)
\(\widehat {DAE} = 120^\circ - 60^\circ = 60^\circ \)
Do đó \(\widehat {BAE} = \widehat {DAE}\) (cùng bằng \(60^\circ \))
Lại có tia \[AE\] nằm giữa hai tia \[AB\] và \[AD\] nên tia \[AE\] là tia phân giác của \(\widehat {BAD}\).
Lời giải
Gọi \(x,y\) (giờ) lần lượt là thời gian người đó đi từ \(A\) đến \(B\) và đi từ \(B\) trở về \(A\).
Vì người đó đi tất cả hết \(7\) giờ nên ta có: \(x + y = 7\).
Do cùng đi một quãng đường nên quãng đường và thời gian đi quãng đường đó là hai đại lượng tỉ lệ nghịch.
Khi đó ta có \(30x = 40y\) hay \(\frac{x}{4} = \frac{y}{3}\).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\frac{x}{4} = \frac{y}{3} = \frac{{x + y}}{{3 + 4}} = \frac{7}{7} = 1\).
Suy ra \(x = 4.1 = 4\); \(y = 3.1 = 3\).
Vậy thời gian người đó đi từ \(A\) đến \(B\) là \(4\) giờ.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.