Giải các phương trình sau:

a) \(\left( { - 2x + 5} \right)\left( {\frac{3}{4}x - 6} \right) = 0\).      

b) \(\frac{{x + 2}}{{x - 2}} = \frac{{x - 2}}{{x + 2}} + \frac{{16}}{{{x^2} - 4}}\).

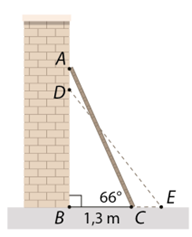
Xét \(\Delta ABC\) vuông tại \(A,\) ta có:

\(BC = AC \cdot \cos C\), suy ra \(AC = \frac{{BC}}{{\cos C}} = \frac{{1,3}}{{\cos 66^\circ }} \approx 3,20\) (m).

Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(AB = BC \cdot \tan C = 1,3 \cdot \tan 66^\circ  \approx 2,92\) (m).

Khi đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}} = 0,4{\rm{\;m}}\) đến vị trí \(D\) thì \(DB = AB - AD \approx 2,92 - 0,4 = 2,52\) (m) và chiều dài thang là \(DE = AC \approx 3,20\) (m).

Xét \(\Delta BDE\) vuông tại \(B,\) ta có:

\(\sin \widehat {DEB} = \frac{{BD}}{{DE}} \approx \frac{{2,52}}{{3,2}} = 0,7875\), suy ra \(\widehat {DEB} \approx 51^\circ 57'.\)

Gọi \(x\) là số lượng khách thứ 51 trở lên, \(x > 0,\,\,x \in \mathbb{N}.\)

Cứ thêm một người thì giá chuyến du lịch còn lại là: \[300\,\,0000 - 50\,\,000 \cdot 1\] đồng/ người cho toàn bộ hành khách.

Thêm \(x\) người thì giá chuyến du lịch còn lại là: \[300\,\,0000 - 50\,\,000x\] đồng/người cho toàn bộ hành khách.

Doanh thu công ty du lịch thu được là:

\(T = \left( {50 + x} \right)\left( {3\,\,000\,\,000 - 50\,\,000x} \right) = 50\,\,000\left( {50 + x} \right)\left( {60 - x} \right)\) (đồng).

Để doanh thu cao nhất thì ta tìm giá trị lớn nhất của biểu thức \(T.\)

⦁ Chứng minh bất đẳng thức: \(ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\,\,\,\,\left( * \right)\) với \(a,\,\,b\) là các số không âm.

Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)

Với mọi \(a,\,\,b\) là các số không âm, ta có:

\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).

Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.

⦁ Áp dụng bất đẳng thức \(\left( * \right)\) vào biểu thức \(T = 50\,\,000\left( {50 + x} \right)\left( {60 - x} \right),\) ta được:

\[T = 50\,\,000\left( {50 + x} \right)\left( {60 - x} \right) \le 50\,\,000 \cdot {\left( {\frac{{50 + x + 60 - x}}{2}} \right)^2} = 151\,\,250\,\,000\].

Dấu “=” xảy ra khi và chỉ khi \[50 + x = 60 - x\] hay \[x = 5\].

Vậy nếu đoàn khách có \(50 + 5 = 55\) người thì công ty du lịch đạt doanh thu cao nhất là \[151\,\,250\,\,000\] đồng.