Giải bài toán sau bằng cách lập hệ phương trình:
Gen B có \(3\,\,600\) liên kết hydrogen và có hiệu giữa nucleotide loại \[T\] với loại nucleotide không bổ sung với nó là \(300\) nucleotide. Tính số nucleotide từng loại của gen B. Biết rằng, để tính số lượng nucleotide \[\left( {A,{\rm{ }}T,{\rm{ }}G,{\rm{ }}C} \right)\] trong phân tử DNA, ta áp dụng nguyên tắc bổ sung: “\[A\] liên kết với \[T\] bằng 2 liên kết hydrogen và \[G\] liên kết với \[C\] bằng 3 liên kết hydrogen” và \(\% A = \% T,\,\,\% G = \% C.\) Tổng số nucleotide trong gen:
\(N = A + T + G + C = 2A + 2G = 2T + 2C.\)
Giải bài toán sau bằng cách lập hệ phương trình:
Gen B có \(3\,\,600\) liên kết hydrogen và có hiệu giữa nucleotide loại \[T\] với loại nucleotide không bổ sung với nó là \(300\) nucleotide. Tính số nucleotide từng loại của gen B. Biết rằng, để tính số lượng nucleotide \[\left( {A,{\rm{ }}T,{\rm{ }}G,{\rm{ }}C} \right)\] trong phân tử DNA, ta áp dụng nguyên tắc bổ sung: “\[A\] liên kết với \[T\] bằng 2 liên kết hydrogen và \[G\] liên kết với \[C\] bằng 3 liên kết hydrogen” và \(\% A = \% T,\,\,\% G = \% C.\) Tổng số nucleotide trong gen:
\(N = A + T + G + C = 2A + 2G = 2T + 2C.\)
Quảng cáo
Trả lời:
Theo bài, hiệu giữa nucleotide loại T với loại nucleotide không bổ sung với nó là \(300\) nucleotide nên ta có phương trình: \(T - G = 300\). (1)
Theo nguyên tắc bổ sung: “\[A\] liên kết với \[T\] bằng 2 liên kết hydrogen và \[G\] liên kết với \[C\] bằng 3 liên kết hydrogen” và theo bài, gen B có \(3\,\,600\) liên kết hydrogen nên ta có phương trình \(2T + 3G = 3\,\,600\). (2)
Từ phương trình (1) và phương trình (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}T - G = 300\\2T + 3G = 3\,\,600\end{array} \right.\)
Nhân hai vế của phương trình thứ nhất với 3, ta được hệ \(\left\{ \begin{array}{l}3T - 3G = 900\\2T + 3G = 3\,\,600\end{array} \right.\)
Cộng từng vế hai phương trình của hệ ta được: \(5T = 4\,500,\) suy ra \(T = 900\).
Thay \(T = 900\) vào phương trình \(T - G = 300\), ta được: \(900 - G = 300,\) suy ra \(G = 600.\)
Vậy số nucleotide từng loại gen B là: \(G = C = 600\) và \(A = T = 900\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giá thuê mỗi phòng sau khi tăng giá phòng lên \[x\% \] là: \(480 + 480 \cdot x\% = 480 + 4,8x\) (nghìn đồng).
Số phòng cho thuê lúc giá phòng tăng \[x\% \] là: O10-2024-GV154..\[100 - 100 \cdot \frac{{4x}}{5}\% \]\[ = 100 - \frac{{4x}}{5}\] (phòng).
Tổng doanh thu tương ứng là:
\[A\left( x \right) = \left( {100 - \frac{{4x}}{5}} \right)\left( {480 + 4,8x} \right)\]\[ = 3,84\left( {125 - x} \right)\left( {100 + x} \right)\] (nghìn đồng).
Để nhà nghỉ đạt doanh thu cao nhất thì ta tìm giá trị lớn nhất của biểu thức \(A\left( x \right)\).
⦁ Chứng minh bất đẳng thức: \(ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\,\,\,\,\left( * \right)\) với \(a,\,\,b\) là các số không âm.
Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)
Với mọi \(a,\,\,b\) là các số không âm, ta có:
\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).
Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.
⦁ Áp dụng bất đẳng thức \(\left( * \right)\) cho biểu thức \(A\left( x \right) = 3,84\left( {125 - x} \right)\left( {100 + x} \right),\) ta được:
\[A\left( x \right) = 3,84\left( {125 - x} \right)\left( {100 + x} \right) \le 3,84 \cdot {\left( {\frac{{125 - x + 100 + x}}{2}} \right)^2} = 48\,\,600\].
Dấu “=” xảy ra khi và chỉ khi \[125 - x = 100 + x\] hay \[x = 12,5\].
Vậy giá phòng niêm yết là \[480 + 4,8 \cdot 12,5 = 540\] (nghìn đồng) thì khách sạn đạt doanh thu cao nhất là \(48\,\,600\) nghìn đồng \((48\,\,600\,\,000\) đồng).
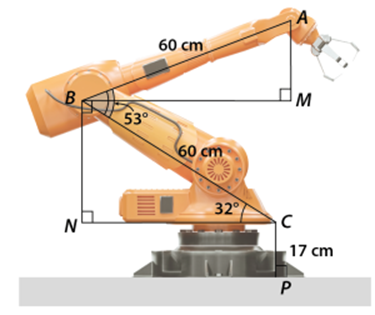
Lời giải
Xét \(\Delta BCN\) vuông tại \(N,\) ta có:
\(BN = BC \cdot \sin \widehat {BCN} = 60 \cdot \sin 32^\circ \approx 31,80{\rm{\;(cm)}}{\rm{.}}\)
Ta thấy \(NC\) và \(BM\) là các đoạn thẳng nằm trên phương ngang nên \(NC\,{\rm{//}}\,BM,\) suy ra \(\widehat {CBM} = \widehat {BCN} = 32^\circ \) (so le trong).
Khi đó, \(\widehat {ABM} = \widehat {ABC} - \widehat {CBM} = 53^\circ - 32^\circ = 21^\circ \).
Xét \(\Delta ABM\) vuông tại \(M\), ta có:
\(AM = AB \cdot \sin \widehat {ABM} = 60 \cdot \sin 21^\circ \approx 21,50\) (cm).
Vậy, độ cao của điểm \(A\) trên đầu cánh tay robot so với mặt đất là:
\(AM + BN + CP \approx 21,50 + 31,80 + 17 = 70,3\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.