Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2ax + by = - 4}\\{bx - ay = 4}\end{array}} \right.\).
a) Với \(a = 1,\,\,\)\(b = 0\) thì tất cả các nghiệm của phương trình \(2ax + by = - 4\) được biểu diễn bởi đồ thị của hàm số nào? Đồ thị này có vị trí như thế nào đối với hai trục tọa độ?
b) Xác định cặp số \(\left( {a;\,\,b} \right)\) để hệ phương trình đã cho có nghiệm là \(\left( {1; - 2} \right).\)
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2ax + by = - 4}\\{bx - ay = 4}\end{array}} \right.\).
a) Với \(a = 1,\,\,\)\(b = 0\) thì tất cả các nghiệm của phương trình \(2ax + by = - 4\) được biểu diễn bởi đồ thị của hàm số nào? Đồ thị này có vị trí như thế nào đối với hai trục tọa độ?
b) Xác định cặp số \(\left( {a;\,\,b} \right)\) để hệ phương trình đã cho có nghiệm là \(\left( {1; - 2} \right).\)
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 9 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
a) Với \(a = 1,\) \(b = 0\), ta có phương trình \(2x = - 4\) hay \(x = - 2.\)
Như vậy với \(a = 1,\) \(b = 0,\) tất cả các nghiệm của phương trình \(2ax + by = - 4\) được biểu diễn bởi đồ thị của hàm số \(x = - 2.\)
Đồ thị hàm số \(x = - 2\) là đường thẳng song song với trục tung và vuông góc với trục hoành tại điểm \( - 2.\)
b) Để hệ phương trình đã cho có nghiệm là \(\left( {1; - 2} \right)\) thì \(x = 1,\,\,y = - 2\) thỏa mãn hệ phương trình đó.
Thay \(x = 1,\,\,y = - 2\) vào hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2ax + by = - 4}\\{bx - ay = 4}\end{array}} \right.\) ta được:
\(\left\{ {\begin{array}{*{20}{c}}{2a \cdot 1 + b \cdot \left( { - 2} \right) = - 4}\\{b \cdot 1 - a \cdot \left( { - 2} \right) = 4}\end{array}} \right.\) hay \(\left\{ \begin{array}{l}2a - 2b = - 4\\2a + b = 4\end{array} \right.\)
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta được:
\( - 3b = - 8\) suy ra \(b = \frac{8}{3}.\)
Thay \(b = \frac{8}{3}\) vào phương trình \(2a + b = 4,\) ta được:
\(2a + \frac{8}{3} = 4,\) suy ra \(a = \frac{2}{3}.\)
Vậy cặp số \(\left( {a;\,\,b} \right)\) cần tìm là \(\left( {\frac{2}{3};\,\,\frac{8}{3}} \right).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (gam) và \(y\) (gam) lần lượt là khối lượng dung dịch muối ăn với nồng độ \(5\% \) và \(20\% \) cần dùng \(\left( {0 < x < 1\,\,000,\,\,0 < y < 1\,\,000} \right)\).
Theo bài, cần pha trộn hai dung dịch trên để được \(1\,\,000\) g dung dịch muối ăn mới nên ta có phương trình \(x + y = 1\,\,000\). (1)
Khối lượng muối ăn trong \(x\) (gam) dung dịch muối ăn \(5\% \) là \(5\% \cdot x = 0,05x\) (gam).
Khối lượng muối ăn trong \(y\) (gam) dung dịch muối ăn \(20\% \) là \(20\% \cdot x = 0,2x\) (gam).
Khối lượng muối ăn trong \(1\,\,000\) gam dung dịch muối ăn \(14\% \) là \(1\,\,000 \cdot 14\% = 140\) (gam).
Khi đó, ta có phương trình: \(0,05x + 0,2y = 140\). (2)
Từ phương trình (1) và phương trình (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 1\,\,000\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\0,05x + 0,2y = 140\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Nhân hai vế của phương trình (2) với 5, ta được hệ mới là \(\left\{ \begin{array}{l}x + y = 1\,\,000\\0,25x + y = 700\end{array} \right.\)
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
\(0,75x = 300,\) suy ra \(x = 400\) (thỏa mãn).
Thay \(x = 400\) vào phương trình (1), ta được: \(400 + y = 1\,\,000\) suy ra \(y = 600\) (thỏa mãn).
Vậy cần trộn \(400\) gam dung dịch muối ăn \(5\% \) với \(600\) gam dung dịch muối ăn \(20\% \) để được \(1\,\,000\) gam dung dịch muối ăn \(14\% .\)
Lời giải
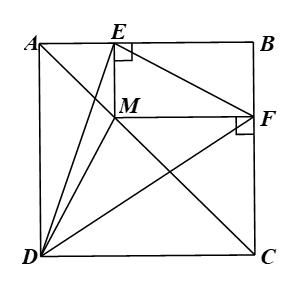
Ta có: \({S_{DEF}} = {S_{DEM}} + {S_{DMF}} + {S_{MEF}};\) \({S_{AEFC}} = {S_{AEM}} + {S_{MFC}} + {S_{MEF}};\)
\({S_{DEM}} = {S_{AEM}}\left( { = \frac{1}{2}AE \cdot EM} \right);\) \({S_{DMF}} = {S_{MFC}}\left( { = \frac{1}{2}FC \cdot FM} \right).\)
Suy ra \({S_{DEF}} = {S_{AEFC}} = {S_{ABC}} - {S_{BEF}} = \frac{1}{2}{S_{ABCD}} - \frac{1}{2}BE \cdot BF\)
Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)
Với mọi \(a,\,\,b\) là các số không âm, ta có:
\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).
Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.
⦁ Áp dụng bất đẳng thức \(\left( * \right)\) vào tích \(BE \cdot BF,\) ta được: \[BE \cdot BF \le {\left( {\frac{{BE + BF}}{2}} \right)^2}.\]
Dấu “=” xảy ra khi và chỉ khi \(BE = BF.\)
Ta có tứ giác \[BEMF\] là hình chữ nhật (do \(\widehat B = \widehat E = \widehat F = 90^\circ )\) nên \(ME = BF.\)
Xét \(\Delta AME\) vuông tại \(E\) có \(\widehat {EAM} = 45^\circ \) (do \(AC\) là đường chéo của hình vuông \(ABCD\) nên \(AC\) là tia phân giác của góc \(\widehat {BAD})\) nên \(\Delta AME\) vuông cân tại \(E\).
Suy ra \(AE = ME.\) Như vậy \(BF = AE.\)
Ta có: \(BE \cdot BF \le {\left( {\frac{{BE + BF}}{2}} \right)^2} = {\left( {\frac{{BE + EA}}{2}} \right)^2} = \frac{{A{B^2}}}{4} = \frac{1}{4}{S_{ABCD}}\)
Suy ra \({S_{DEF}} \ge \frac{1}{2}{S_{ABCD}} - \frac{1}{8}{S_{ABCD}} = \frac{3}{8}{S_{ABCD}}.\) (đơn vị diện tích).
Dấu “=” xảy ra khi và chỉ khi \(BE = BF = AE\) hay \(E\) là trung điểm của \(AB,\) lúc này từ tính chất đường trung bình ta suy ra được điểm \(M\) phải là trung điểm của \(AC\).
Vậy nếu \(M\) là trung điểm của \(AC\) thì tam giác \(DEF\) có diện tích nhỏ nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Lúc 6 giờ sáng, bạn An đi từ nhà (điểm \[A)\] đến trường (điểm \[B)\] phải leo lên và xuống một con dốc đỉnh \(C\) được mô tả như hình vẽ dưới. Cho biết đoạn \[AB\] dài 762 m, \(\widehat {A\,\,} = 4^\circ ,\,\,\widehat {B\,} = 6^\circ .\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/screenshot-2025-11-25-212010-1764080274.png)