Một người đang ở trên tầng thượng của một tòa nhà quan sát con đường chạy thẳng đến chân tòa nhà. Anh ta nhìn thấy một người điều khiển chiếc xe máy đi về phía tòa nhà với phương nhìn tạo với phương nằm ngang một góc bằng \[30^\circ \]. Sau \[6\] phút, người quan sát vẫn nhìn thấy người điều khiển chiếc xe máy với phương nhìn tạo với phương nằm ngang một góc bằng \[60^\circ \]. Hỏi sau bao nhiêu phút nữa thì xe máy sẽ chạy đến chân tòa nhà? Cho biết vận tốc xe máy không đổi.
Một người đang ở trên tầng thượng của một tòa nhà quan sát con đường chạy thẳng đến chân tòa nhà. Anh ta nhìn thấy một người điều khiển chiếc xe máy đi về phía tòa nhà với phương nhìn tạo với phương nằm ngang một góc bằng \[30^\circ \]. Sau \[6\] phút, người quan sát vẫn nhìn thấy người điều khiển chiếc xe máy với phương nhìn tạo với phương nằm ngang một góc bằng \[60^\circ \]. Hỏi sau bao nhiêu phút nữa thì xe máy sẽ chạy đến chân tòa nhà? Cho biết vận tốc xe máy không đổi.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta mô hình hóa bài toán như hình vẽ sau:
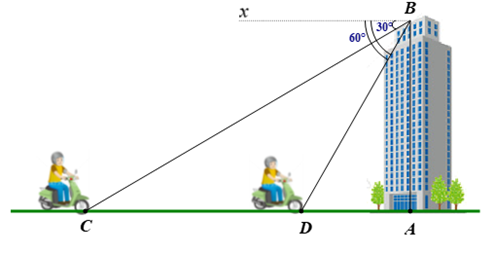
Do mặt đất là phương ngang nên \[\widehat {BCA} = \widehat {CBx} = 30^\circ \] và \[\widehat {BDA} = \widehat {ABx} - \widehat {DBx} = 90^\circ - 30^\circ = 60^\circ \].
Xét \[\Delta ABC\] vuông tại \[A\], ta có:
\[AC = AB \cdot \cot \widehat {BCA} = AB \cdot \cot 30^\circ = AB\sqrt 3 \].
Xét \[\Delta ABD\] vuông tại \[A\], ta có:
\[AD = AB \cdot \cot \widehat {BDA} = AB \cdot \cot 60^\circ = \frac{{AB\sqrt 3 }}{3}\].
Suy ra \[CD = AC - AD = AB\sqrt 3 - \frac{{AB\sqrt 3 }}{3} = AB\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right) = AB \cdot \frac{{2\sqrt 3 }}{3} = \frac{{2AB\sqrt 3 }}{3} = 2AD\].
Như vậy, quãng đường \(CD\) gấp đôi quãng đường \(DA.\) Mà thời gian di chuyển tỉ lệ thuận với quãng đường đi được khi vận tốc không đổi nên thời gian xe máy di chuyển từ \(C\) đến \(D\) gấp đôi thời gian xe máy di chuyển từ \(D\) về \(A\).
Vậy thời gian để xe máy chạy từ \[D\] đến tòa nhà là \[\frac{6}{2} = 3\] (phút).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Với chế độ ăn kiêng và luyện tập hợp lí, chị Hương có thể giảm \(0,5\) kg mỗi tuần thì số kg chị Hương giảm được sau \(x\) tuần là: \(0,5x\) (kg).
Cân nặng của chị Hương sau \(x\) tuần là: \(55 - 0,5x\) (kg).
Theo bài, chị Hương muốn giảm cân sao cho cân nặng của mình không lớn hơn 45 kg nên ta có bất phương trình: \(55 - 0,5x \le 45\).
Vậy từ dữ kiện đề bài, ta viết được bất phương trình: \(55 - 0,5x \le 45\).
b) Giải bất phương trình:
\(55 - 0,5x \le 45\)
\(10 \le 0,5x\)
\(x \ge 20\).
Vậy chị Hương phải thực hiện chế độ ăn kiêng và luyện tập ít nhất 20 tuần để đạt được mục tiêu của mình.
Lời giải
a) \[ - 4x + 3 \le 3x - 1\]
\[ - 4x - 3x \le - 1 - 3\]
\[ - 7x \le - 4\]
\[x \ge \frac{4}{7}.\]
Vậy nghiệm của bất phương trình đã cho là \[x \ge \frac{4}{7}.\]
b) \[\frac{{4x + 1}}{3} - \frac{{x - 5}}{4} \ge \frac{1}{2} - \frac{{3 - x}}{5}\]
\[\frac{{20\left( {4x + 1} \right)}}{{60}} - \frac{{15\left( {x - 5} \right)}}{{60}} \ge \frac{{30 \cdot 1}}{{60}} - \frac{{12\left( {3 - x} \right)}}{{60}}\]
\[20\left( {4x + 1} \right) - 15\left( {x - 5} \right) \ge 30 \cdot 1 - 12\left( {3 - x} \right)\]
\[80x + 20 - 15x + 75 \ge 30 - 36 + 12x\]
\[65x + 95 \ge - 6 + 12x\]
\[53x \ge - 101\]
\[x \ge - \frac{{101}}{{53}}\].
Vậy nghiệm của bất phương trình đã cho là \[x \ge - \frac{{101}}{{53}}\].Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập