Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2ax + by = - 4}\\{bx - ay = 4}\end{array}} \right.\).
a) Với \(a = 1,\,\,\)\(b = 0\) thì tất cả các nghiệm của phương trình \(2ax + by = - 4\) được biểu diễn bởi đồ thị của hàm số nào? Đồ thị này có vị trí như thế nào đối với hai trục tọa độ?
b) Xác định cặp số \(\left( {a;\,\,b} \right)\) để hệ phương trình đã cho có nghiệm là \(\left( {1; - 2} \right).\)
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2ax + by = - 4}\\{bx - ay = 4}\end{array}} \right.\).
a) Với \(a = 1,\,\,\)\(b = 0\) thì tất cả các nghiệm của phương trình \(2ax + by = - 4\) được biểu diễn bởi đồ thị của hàm số nào? Đồ thị này có vị trí như thế nào đối với hai trục tọa độ?
b) Xác định cặp số \(\left( {a;\,\,b} \right)\) để hệ phương trình đã cho có nghiệm là \(\left( {1; - 2} \right).\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Với \(a = 1,\) \(b = 0\), ta có phương trình \(2x = - 4\) hay \(x = - 2.\)
Như vậy với \(a = 1\,,\,\,b = 0,\) tất cả các nghiệm của phương trình \(2ax + by = - 4\) được biểu diễn bởi đồ thị của hàm số \(x = - 2.\)
Đồ thị hàm số \(x = - 2\) là đường thẳng song song với trục tung và vuông góc với trục hoành tại điểm \( - 2.\)
b) Để hệ phương trình đã cho có nghiệm là \(\left( {1; - 2} \right)\) thì \(x = 1,\,\,y = - 2\) thỏa mãn hệ phương trình đó.
Thay \(x = 1,\,\,y = - 2\) vào hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{2ax + by = - 4}\\{bx - ay = 4}\end{array}} \right.\) ta được:
\(\left\{ {\begin{array}{*{20}{c}}{2a \cdot 1 + b \cdot \left( { - 2} \right) = - 4}\\{b \cdot 1 - a \cdot \left( { - 2} \right) = 4}\end{array}} \right.\) hay \(\left\{ \begin{array}{l}2a - 2b = - 4\\2a + b = 4\end{array} \right.\)
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta được:
\( - 3b = - 8\) suy ra \(b = \frac{8}{3}.\)
Thay \(b = \frac{8}{3}\) vào phương trình \(2a + b = 4,\) ta được: \(2a + \frac{8}{3} = 4,\) suy ra \(a = \frac{2}{3}.\)
Vậy cặp số \(\left( {a;\,\,b} \right)\) cần tìm là \(\left( {\frac{2}{3};\,\,\frac{8}{3}} \right).\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
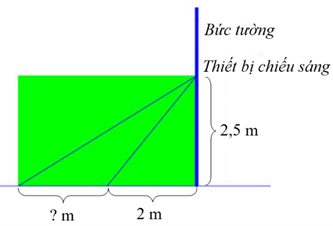
Xét \(\Delta ABC\) vuông tại \(B\), ta có
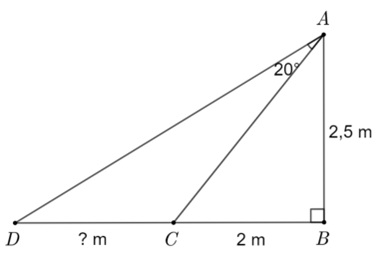
\(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{2}{{2,5}} = 0,8\) nên \(\widehat {BAC} \approx 38,7^\circ .\)
Ta có \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx 38,7^\circ + 20^\circ = 58,7^\circ .\)
Xét \(\Delta ABD\) vuông tại \(B\), ta có
\(BD = AB \cdot \tan \widehat {BAD} \approx 2,5 \cdot \tan 58,7^\circ \approx 4,1\,\,\left( {\rm{m}} \right).\)Do đó \(CD = BD - BC \approx 4,1 - 2 = 2,1\,\,\left( {\rm{m}} \right).\)
Vậy độ dài vùng được chiếu sáng trên mặt đất khoảng \(2,1\) mét.
Lời giải
a) Đổi \(5,25\) tấn \( = 5\,\,250\,\,{\rm{kg}}\).
Gọi \(x\) (thùng) là số sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\).
Khi đó, khối lượng sữa mà xe chở là: \(10x\,\,\left( {{\rm{kg}}} \right).\)
Tổng khối lượng sữa và bác tài xế là: \(65 + 10x\,\,\left( {{\rm{kg}}} \right).\)
Do trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5\,\,250\,\,{\rm{kg}}\) nên ta có
\(65 + 10x \le 5\,\,250\)
Vậy bất phương trình cần tìm là: \(65 + 10x \le 5\,\,250\).
b) Giải bất phương trình:
\(65 + 10x \le 5\,\,250\)
\(10x \le 5\,\,185\)
\(x \le 518,5\)
Mà \(x \in \mathbb{N}*\) nên xe tải đó có thể chở tối đa 518 thùng sữa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập