Giải các bất phương trình sau:
a) \(9x + 7 >- 12x - 1\).
b) \[\frac{{2x + 1}}{3} - \frac{{x - 4}}{4} \le \frac{{3x + 1}}{6} - \frac{{x - 4}}{{12}}.\]
Giải các bất phương trình sau:
a) \(9x + 7 >- 12x - 1\).
b) \[\frac{{2x + 1}}{3} - \frac{{x - 4}}{4} \le \frac{{3x + 1}}{6} - \frac{{x - 4}}{{12}}.\]
Quảng cáo
Trả lời:
a) \(9x + 7 \ge - 12x - 1\)
\(9x + 12x \ge - 1 - 7\)
\(21x \ge - 8\)
\(x \ge \frac{{ - 8}}{{21}}\)
Vậy bất phương trình đã cho có nghiệm là \(x \ge \frac{{ - 8}}{{21}}.\)b) \[\frac{{2x + 1}}{3} - \frac{{x - 4}}{4} \le \frac{{3x + 1}}{6} - \frac{{x - 4}}{{12}}\]
\[\frac{{4\left( {2x + 1} \right)}}{{12}} - \frac{{3\left( {x - 4} \right)}}{{12}} \le \frac{{2\left( {3x + 1} \right)}}{{12}} - \frac{{x - 4}}{{12}}\]
\[4\left( {2x + 1} \right) - 3\left( {x - 4} \right) \le 2\left( {3x + 1} \right) - \left( {x - 4} \right)\]
\[8x + 4 - 3x + 12 \le 6x + 2 - x + 4\]
\[5x + 16 \le 5x + 6\]
\[5x - 5x \le 6 - 16\]
\[0x \le - 10\].
Vậy bất phương trình đã cho vô nghiệm.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét \(\Delta ABC\) vuông tại \(B\), ta có
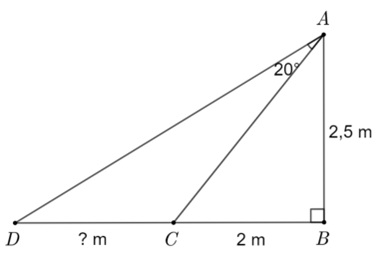
\(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{2}{{2,5}} = 0,8\) nên \(\widehat {BAC} \approx 38,7^\circ .\)
Ta có \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx 38,7^\circ + 20^\circ = 58,7^\circ .\)
Xét \(\Delta ABD\) vuông tại \(B\), ta có
\(BD = AB \cdot \tan \widehat {BAD} \approx 2,5 \cdot \tan 58,7^\circ \approx 4,1\,\,\left( {\rm{m}} \right).\)Do đó \(CD = BD - BC \approx 4,1 - 2 = 2,1\,\,\left( {\rm{m}} \right).\)
Vậy độ dài vùng được chiếu sáng trên mặt đất khoảng \(2,1\) mét.
Lời giải
a) Đổi \(5,25\) tấn \( = 5\,\,250\,\,{\rm{kg}}\).
Gọi \(x\) (thùng) là số sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\).
Khi đó, khối lượng sữa mà xe chở là: \(10x\,\,\left( {{\rm{kg}}} \right).\)
Tổng khối lượng sữa và bác tài xế là: \(65 + 10x\,\,\left( {{\rm{kg}}} \right).\)
Do trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5\,\,250\,\,{\rm{kg}}\) nên ta có
\(65 + 10x \le 5\,\,250\)
Vậy bất phương trình cần tìm là: \(65 + 10x \le 5\,\,250\).
b) Giải bất phương trình:
\(65 + 10x \le 5\,\,250\)
\(10x \le 5\,\,185\)
\(x \le 518,5\)
Mà \(x \in \mathbb{N}*\) nên xe tải đó có thể chở tối đa 518 thùng sữa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.