Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại \(180\,\,{\rm{ml}}\) nặng trung bình \(10\,\,{\rm{kg}}.\) Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5,25\) tấn.
a) Gọi \(x\) là số thùng sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\). Viết bất phương trình phù hợp với dữ liệu đề bài.
b) Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng \(65\,\,kg?\)
Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại \(180\,\,{\rm{ml}}\) nặng trung bình \(10\,\,{\rm{kg}}.\) Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5,25\) tấn.
a) Gọi \(x\) là số thùng sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\). Viết bất phương trình phù hợp với dữ liệu đề bài.
b) Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng \(65\,\,kg?\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đổi \(5,25\) tấn \( = 5\,\,250\,\,{\rm{kg}}\).
Gọi \(x\) (thùng) là số sữa mà xe có thể chở \(\left( {x \in \mathbb{N}*} \right)\).
Khi đó, khối lượng sữa mà xe chở là: \(10x\,\,\left( {{\rm{kg}}} \right).\)
Tổng khối lượng sữa và bác tài xế là: \(65 + 10x\,\,\left( {{\rm{kg}}} \right).\)
Do trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5\,\,250\,\,{\rm{kg}}\) nên ta có
\(65 + 10x \le 5\,\,250\)
Vậy bất phương trình cần tìm là: \(65 + 10x \le 5\,\,250\).
b) Giải bất phương trình:
\(65 + 10x \le 5\,\,250\)
\(10x \le 5\,\,185\)
\(x \le 518,5\)
Mà \(x \in \mathbb{N}*\) nên xe tải đó có thể chở tối đa 518 thùng sữa.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét \(\Delta ABC\) vuông tại \(B\), ta có
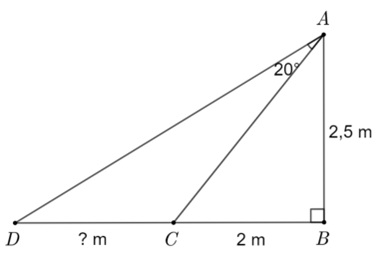
\(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{2}{{2,5}} = 0,8\) nên \(\widehat {BAC} \approx 38,7^\circ .\)
Ta có \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx 38,7^\circ + 20^\circ = 58,7^\circ .\)
Xét \(\Delta ABD\) vuông tại \(B\), ta có
\(BD = AB \cdot \tan \widehat {BAD} \approx 2,5 \cdot \tan 58,7^\circ \approx 4,1\,\,\left( {\rm{m}} \right).\)Do đó \(CD = BD - BC \approx 4,1 - 2 = 2,1\,\,\left( {\rm{m}} \right).\)
Vậy độ dài vùng được chiếu sáng trên mặt đất khoảng \(2,1\) mét.
Lời giải
a) \[2x(3x - 1) + 6x - 2 = 0\]
\[2x\left( {3x - 1} \right) + 2\left( {3x - 1} \right) = 0\]
\[\left( {3x - 1} \right)\left( {2x + 2} \right) = 0\]
\[2\left( {3x - 1} \right)\left( {x + 1} \right) = 0\]
\(3x - 1 = 0\) hoặc \(x + 1 = 0\)
\(x = \frac{1}{3}\) hoặc \(x = - 1\).
Vậy nghiệm của phương trình là \(x = \frac{1}{3}\) và \(x = - 1.\)
b) Điều kiện xác định: \(x \ne 0,\,\,x \ne 2,\,\,x \ne - 2.\)
\(\frac{2}{{{x^2} - 4}} - \frac{{x - 1}}{{x\left( {x - 2} \right)}} + \frac{{x - 4}}{{x\left( {x + 2} \right)}} = 0\)
\(\frac{{2x}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{\left( {x - 4} \right)\left( {x - 2} \right)}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}} = 0\)
\(2x - \left( {x - 1} \right)\left( {x + 2} \right) + \left( {x - 4} \right)\left( {x - 2} \right) = 0\)
\(2x - \left( {{x^2} + 2x - x - 2} \right) + \left( {{x^2} - 2x - 4x + 8} \right) = 0\)
\(2x - \left( {{x^2} + x - 2} \right) + \left( {{x^2} - 6x + 8} \right) = 0\)
\(2x - {x^2} - x + 2 + {x^2} - 6x + 8 = 0\)
\( - 5x + 10 = 0\)
\( - 5x = - 10\)
\(x = 2\) (không thỏa mãn điều kiện).
Vậy phương trình đã cho vô nghiệm.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập