Giải các phương trình sau:
a) \[2x\left( {3x - 1} \right) = \left( {3x - 1} \right).\]
b) \(\frac{{x + 3}}{{x - 3}} = \frac{3}{{{x^2} - 3x}} + \frac{1}{x}.\)
Giải các phương trình sau:
a) \[2x\left( {3x - 1} \right) = \left( {3x - 1} \right).\]
b) \(\frac{{x + 3}}{{x - 3}} = \frac{3}{{{x^2} - 3x}} + \frac{1}{x}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) \[2x\left( {3x - 1} \right) = \left( {3x - 1} \right)\]
\(2x\left( {3x - 1} \right) - \left( {3x - 1} \right) = 0\)
\(\left( {3x - 1} \right)\left( {2x - 1} \right) = 0\)
\(3x - 1 = 0\) hoặc \(2x - 1 = 0\)
\(x = \frac{1}{3}\) hoặc \(x = \frac{1}{2}\).
Vậy nghiệm của phương trình là \(x = \frac{1}{3}\) và \(x = \frac{1}{2}\).
b) Điều kiện xác định \(x \ne 0;\,\,x \ne 3.\)
\(\frac{{x + 3}}{{x - 3}} = \frac{3}{{{x^2} - 3x}} + \frac{1}{x}\)
\(\frac{{\left( {x + 3} \right)x}}{{x\left( {x - 3} \right)}} = \frac{3}{{x\left( {x - 3} \right)}} + \frac{{x - 3}}{{x\left( {x - 3} \right)}}\)
\(\left( {x + 3} \right)x = 3 + x - 3\)
\({x^2} + 3x = 3 + x - 3\)
\({x^2} + 2x = 0\)
\(x\left( {x + 2} \right) = 0\)
\(x = 0\) hoặc \(x + 2 = 0\)
\(x = 0\) hoặc \(x = - 2\).
Đối chiếu ĐKXĐ suy ra nghiệm phương trình đã cho là \(x = - 2\).Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Giả sử trong hình vẽ \(BC\) là độ cao của ngọn hải đăng so với mực nước biển thì \(AB\) là khoảng cách từ tàu đến chân ngọn hải đăng, góc nghiêng xuống \[\widehat {ACx} = 27^\circ \] nên \[\widehat {CAB} = 27^\circ .\]
Xét \(\Delta ABC\) vuông tại \(B\) có \(AB = BC \cdot \cot \widehat {CAB}\).
Suy ra \[AB = 149 \cdot \cot 27^\circ \approx 292\,\,\left( {\rm{m}} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(x\) là số lượng khách đăng ký thêm, \(x > 0,\,\,x \in \mathbb{N}.\)
Khi đó, tổng số khách sẽ là \(80 + x\) (khách).
Cứ thêm một người thì giá chuyến du lịch còn lại là: \[5\,\,000\,\,000 - 50\,\,000 \cdot 1\] đồng/ người cho toàn bộ hành khách.
Thêm \(x\) người thì giá chuyến du lịch còn lại là: \[5\,\,000\,\,000 - 50\,\,000x\] đồng/người cho toàn bộ hành khách.
Doanh thu công ty du lịch thu được là:
\(T = \left( {80 + x} \right)\left( {5\,\,000\,\,000 - 50\,\,000x} \right) = 50\,\,000\left( {80 + x} \right)\left( {100 - x} \right)\) (đồng).
Để doanh thu cao nhất thì ta tìm giá trị lớn nhất của biểu thức \(T.\)
⦁ Chứng minh bất đẳng thức: \(ab \le {\left( {\frac{{a + b}}{2}} \right)^2}\,\,\,\,\left( * \right)\) với \(a,\,\,b\) là các số không âm.
Thật vậy, xét hiệu \({\left( {\frac{{a + b}}{2}} \right)^2} - ab = \frac{{{a^2} + 2ab + {b^2} - 4ab}}{4} = \frac{{{a^2} - 2ab + {b^2}}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{2}\)
Với mọi \(a,\,\,b\) là các số không âm, ta có:
\({\left( {a - b} \right)^2} \ge 0\) nên \(\frac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) suy ra \({\left( {\frac{{a + b}}{2}} \right)^2} \ge ab\).
Dấu “=” xảy ra khi và chỉ khi \(a = b.\) Như vậy bất đẳng thức \(\left( * \right)\) đã được chứng minh.
⦁ Áp dụng bất đẳng thức \(\left( * \right)\) vào biểu thức \(T = 50\,\,000\left( {80 + x} \right)\left( {100 - x} \right),\) ta được:
\[T = 50\,\,000\left( {80 + x} \right)\left( {100 - x} \right) \le 20\,\,000 \cdot {\left( {\frac{{80 + x + 100 - x}}{2}} \right)^2} = 648\,\,000\,\,000\].
Dấu “=” xảy ra khi và chỉ khi \[80 + x = 100 - x\] hay \[x = 10\].
Vậy nếu đoàn khách có \(80 + 10 = 90\) người thì công ty du lịch đạt doanh thu cao nhất là \[648\,\,000\,\,000\] đồng.
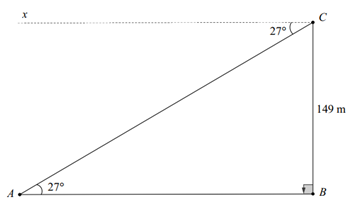
Câu 4
Cho tam giác nhọn \[ABC\] có đường cao \[AK\].
a) Viết các tỉ số lượng giác của góc \(C.\)
b) Chứng minh rằng \[AK = \frac{{BC}}{{\cot B + \cot C}}\].
c) Vẽ hình chữ nhật \[CKAD\], \[BD\] cắt \[AK\] tại \[N\]. Chứng minh rằng \[\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}ACB}}{{D{N^2}}} + \frac{1}{{D{B^2}}}\].
Cho tam giác nhọn \[ABC\] có đường cao \[AK\].
a) Viết các tỉ số lượng giác của góc \(C.\)
b) Chứng minh rằng \[AK = \frac{{BC}}{{\cot B + \cot C}}\].
c) Vẽ hình chữ nhật \[CKAD\], \[BD\] cắt \[AK\] tại \[N\]. Chứng minh rằng \[\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}ACB}}{{D{N^2}}} + \frac{1}{{D{B^2}}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập