Rút gọn biểu thức \(P = \frac{{\sin x + \sin 2x + \sin 3x}}{{\cos x + \cos 2x + \cos 3x}}\).

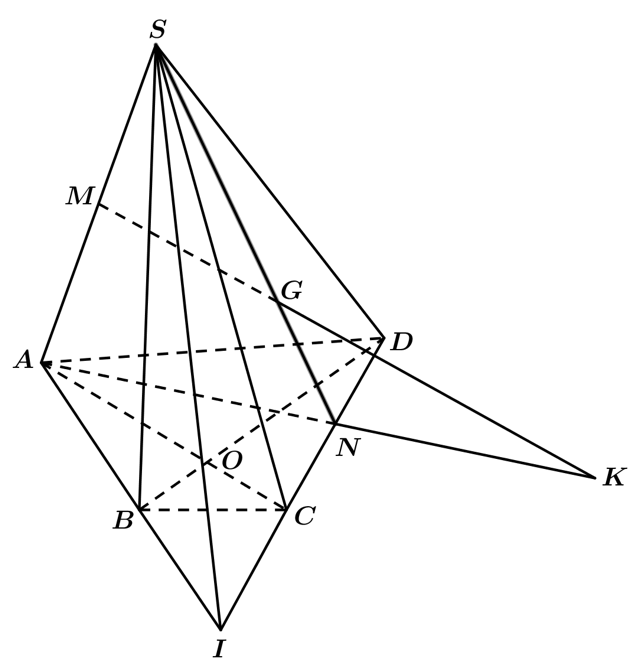
a) Tìm giao tuyến của các cặp mặt phẳng sau: \(\left( {SAC} \right)\) và  \(\left( {SBD} \right)\) ; \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).

+) Gọi \(O\) là giao điểm của \(AC\)và \(BD\)

Ta có:

\(\left\{ \begin{array}{l}O \in AC\\AC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow O \in \left( {SAC} \right)\)

\(\left\{ \begin{array}{l}O \in BD\\BD \subset \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SBD} \right)\)

Mà: \(S \in \left( {SAC} \right)\) và \(S \in \left( {SBD} \right)\)

Vậy: \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO\)

+) Trong mặt phẳng \(\left( {ABCD} \right)\), kéo dài \(AB\)và \(CD\) cắt nhau tại \(I\)

Ta có:

\(\left\{ \begin{array}{l}I \in AB\\AB \subset \left( {SAB} \right)\end{array} \right. \Rightarrow I \in \left( {SAB} \right)\)

\(\left\{ \begin{array}{l}I \in CD\\CD \subset \left( {SCD} \right)\end{array} \right. \Rightarrow I \in \left( {SCD} \right)\)

Mà: \(S \in \left( {SAB} \right)\) và \(S \in \left( {SCD} \right)\)

Vậy: \(\left( {SAB} \right) \cap \left( {SCD} \right) = SI\)

b) Tìm giao điểm của đường thẳng \(MG\) và mặt phẳng \(\left( {ABCD} \right)\).

Gọi \(N\)là trung điểm của \(CD\)

Trong \(\Delta SAN\)có: \(\frac{{SM}}{{SA}} = \frac{1}{2}\;\;;\;\;\frac{{SG}}{{SN}} = \frac{2}{3}\; \Rightarrow \frac{{SM}}{{SA}} \ne \frac{{SG}}{{SN}}\)

\( \Rightarrow \)\(MG\) không song song với \(AI\)

Trong \(\left( {SAI} \right)\), kéo dài \(MG\) và \(AI\) cắt nhau tại \(K\)

Ta có: \(\left\{ \begin{array}{l}K \in AI\\AI \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow K \in \left( {ABCD} \right)\)

Vậy: \(K\) là giao điểm của \(MG\) và \(\left( {ABCD} \right)\)

Chọn C

Ta có \[{u_n} = {u_1}.{q^{n - 1}}\]

Suy ra \( - 3072 =  - {3.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = 1024 = {2^{10}} \Leftrightarrow n - 1 = 10 \Leftrightarrow n = 11.\)

Vây: Số \( - 3072\) là số hạng thứ 11 của cấp số nhân đã cho.