Cho tam giác \(ABC\) có \(AB < AC\). Kẻ tia phân giác \(AD\) của góc \(BAC\) (\(D\) thuộc cạnh \(BC\)). Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AE = AB\), trên tia \(AB\) lấy điểm \(F\) sao cho \(AF = AC\).
a) Chứng minh \[\Delta BDF = \Delta EDC\].
b) Chứng minh ba điểm \(F,\,D,\,E\) thẳng hàng
c) Chứng minh \(AD\) là đường trung trực của \(BE\) và \(CF\).
Cho tam giác \(ABC\) có \(AB < AC\). Kẻ tia phân giác \(AD\) của góc \(BAC\) (\(D\) thuộc cạnh \(BC\)). Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AE = AB\), trên tia \(AB\) lấy điểm \(F\) sao cho \(AF = AC\).
a) Chứng minh \[\Delta BDF = \Delta EDC\].
b) Chứng minh ba điểm \(F,\,D,\,E\) thẳng hàng
c) Chứng minh \(AD\) là đường trung trực của \(BE\) và \(CF\).
Quảng cáo
Trả lời:
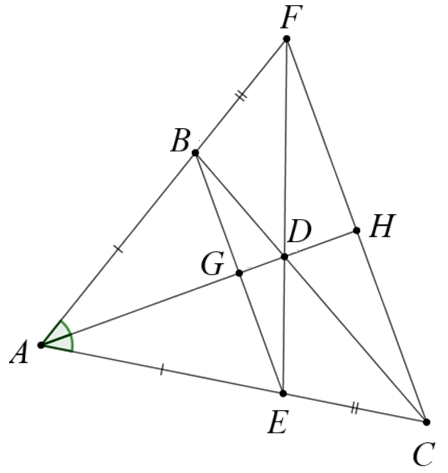
a) Chứng minh \(\Delta BDF = \Delta EDC\).
Vì \(AD\) là phân giác \(\widehat {BAC}\) nên \(\widehat {BAD} = \widehat {CAD}\).
Xét \(\Delta ADF\) và \(\Delta ADC\) có:
\(AF = AC\,;\,\,\widehat {FAD} = \widehat {CAD}\,;\,\,AD\) chung.
Do đó \(\Delta ADF = \Delta ADC\) (c.g.c)
Suy ra \(\widehat {AFD} = \widehat {ACD}\) (hai góc tương ứng) và \(FD = CD\) (hai cạnh tương ứng)
Vì \(AF = AC\,;\,\,AB = AE\) suy ra \(BF = EC\)
Xét tam giác \(BDF\) và tam giác \(EDC\) có:
\(BF = EC\,;\,\,\,\widehat {BFD} = \widehat {ECD}\,;\,\,\,FD = CD\).
Do đó \(\Delta BDF = \Delta EDC\) (c.g.c)
b) Theo câu a) \(\Delta BDF = \Delta EDC\) suy ra \(\widehat {BDF} = \widehat {ECD}\).
Mà \(\widehat {BDE} + \widehat {EDC} = 180^\circ \) (hai góc kề bù) nên\(\widehat {BDE} + \widehat {FDB} = 180^\circ \), do đó \(\widehat {FDE} = 180^\circ \).
Suy ra ba điểm \(F,\,D,\,E\) thẳng hàng.
c) Gọi \(G,\,H\) theo thứ tự là giao điểm của \(AD\) và \(BE,\,CF\).
Xét tam giác \(ABG\) và \(AEG\) có:
\(AB = AE\,;\,\,\widehat {BAG} = \widehat {EAG}\,;\,\,AG\) chung.
Suy ra \(\Delta ABG = \Delta AEG\) (c.g.c)
Do đó, \(\widehat {AGB} = \widehat {AGE}\) (hai góc tương ứng) và \(GB = GE\) (hai cạnh tương ứng) (1)
Mà \(\widehat {AGB} + \widehat {AGE} = 180^\circ \) suy ra \(\widehat {AGB} = \widehat {AGE} = 90^\circ \) (2)
Từ (1) và (2) suy ra \(AD\) là đường trung trực \(BE\).
Chứng minh tương tự ta có \(AD\) là đường trung trực \(CF\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
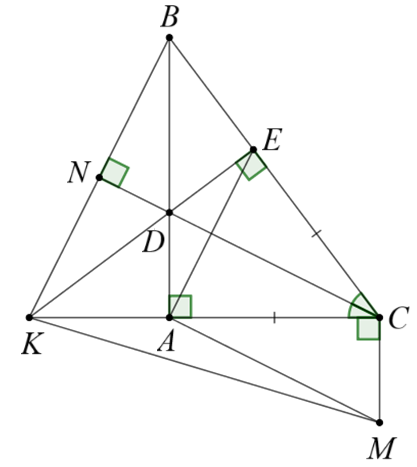
a) Vì \(CD\) là phân giác \(\widehat {BCA}\) suy ra \(\widehat {BCD} = \widehat {ACD}\).
Xét \(\Delta ACD\) và \(\Delta ECD\) có:
\(AC = AF\,;\,\,\widehat {BCD} = \widehat {ACD}\,;\,\,CD\) chung.
Do đó \(\Delta ACD = \Delta ECD\) (c.g.c).
Suy ra \(\widehat {CED} = \widehat {CAD} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DE \bot BC\).
b) Vì \(AM\parallel CD\) suy ra \(\widehat {MAC} = \widehat {DCA}\) (hai góc so le trong)
Vì \(CM \bot CA\) nên \(\widehat {MCA} = 90^\circ \).
Xét \(\Delta CAD\) và \(\Delta ACM\) có:
\(\widehat {DAC} = \widehat {MCA} = 90^\circ \,;\,\,CA\) chung; \(\widehat {DCA} = \widehat {MAC}\).
Do đó \(\Delta CAD = \Delta ACM\) (g.c.g).
Suy ra (hai cạnh tương ứng).
c) Xét tam giác \(NBC\) và tam giác \(NKC\) có:
\(\widehat {BNC} = \widehat {KNC} = 90^\circ \,;\,\,NC\) chung; \(\widehat {BCN} = \widehat {CKN}\)
Suy ra \(\Delta NBC = \Delta NKC\,\)(g.c.g)
Do đó \(\widehat {NBC} = \widehat {NKC}\,;\,\,NB = NK\).
Xét tam giác \(NBD\) và tam giác \(NKD\) có:
\(NB = ND\,;\,\,\widehat {BND} = \widehat {KND}\,;\,\,ND\) chung.
Suy ra \(\Delta NBD = \Delta NKD\) (c.g.c).
Do đó, \(\widehat {NBD} = \widehat {NKD}\) (hai góc tương ứng)
d) Xét tam giác \(BKE\) và tam giác \(BKC\) có:
\[\widehat {BKE} = \widehat {BKA}\,;\,\,BK\] chung; \[\widehat {BKE} = \widehat {KBA}\].
Do đó \(\Delta BKE = \Delta BKC\) (g.c.g)
Suy ra \(\widehat {BEK} = \widehat {KAB} = 90^\circ \) (hai góc tương ứng)
Suy ra \(KE \bot BC\).
Mà \(DE \bot AC\).
Suy ra ba điểm \(K,\,D,\,E\) thẳng hàng.
Câu 2
Cho \(\Delta ABC\) có \(AB < AC\,\). Kẻ \(AH\) vuông góc với \(BC(\,H \in BC)\). Trên tia \(AH\) lấy điểm \(K\) sao cho \(H\) là trung điểm của \(AK\).
a) chứng minh: \(\Delta AHC = \Delta KCH\).
b) Gọi \(E\) là trung điểm của \(BC\). Trên tia \(AE\) lấy điểm \(D\) sao cho \(E\) là trung điểm của \(AD\). Chứng minh rằng: \(BD = AC = CK\).
c) chứng minh rằng: \(EH\) là tia phân giác của góc \(\widehat {AEK}\) và \(DK\,{\rm{//}}\,BC\).
d) Gọi \(I\) là giao điểm của \(BD\) và \(CK\), \(N\) là trung điểm của \(KD\). Chứng minh: \(E,I,N\) thẳng hàng.
Cho \(\Delta ABC\) có \(AB < AC\,\). Kẻ \(AH\) vuông góc với \(BC(\,H \in BC)\). Trên tia \(AH\) lấy điểm \(K\) sao cho \(H\) là trung điểm của \(AK\).
a) chứng minh: \(\Delta AHC = \Delta KCH\).
b) Gọi \(E\) là trung điểm của \(BC\). Trên tia \(AE\) lấy điểm \(D\) sao cho \(E\) là trung điểm của \(AD\). Chứng minh rằng: \(BD = AC = CK\).
c) chứng minh rằng: \(EH\) là tia phân giác của góc \(\widehat {AEK}\) và \(DK\,{\rm{//}}\,BC\).
d) Gọi \(I\) là giao điểm của \(BD\) và \(CK\), \(N\) là trung điểm của \(KD\). Chứng minh: \(E,I,N\) thẳng hàng.
Lời giải
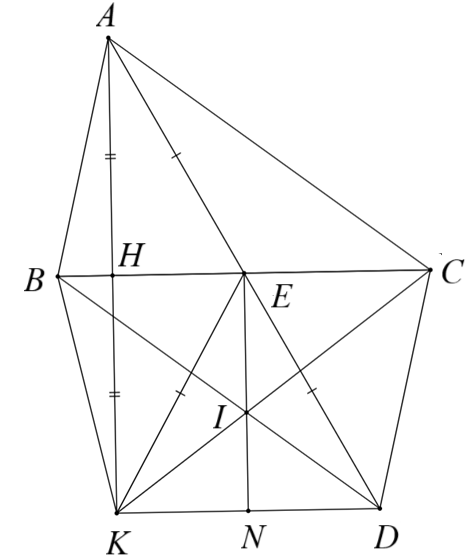
a) Xét \(\Delta AHC\) và \(\Delta KCH\) có
\(AH = HK\) (\(H\) là trung điểm của \(AK\))
\(\widehat {AHC} = \widehat {CHK}\) (\(AH \bot BC\))
\(CH\) là cạnh chung
Do đó \(\Delta AHC = \Delta KHC\) (cgc).
b) Vì \[\Delta AHC = \Delta KHC\] (chứng minh trên) do đó \[AC = CK\] (2 cạnh tương ứng) (1)
Xét \[\Delta AEC\] và \[\Delta DEB\] ta có :
\[AE = ED\] (\[E\] là trung điểm của \[AD\])
\[BE = CE\] (\[E\] là trung điểm của \[BE\]) \[\widehat {AEC} = \widehat {BEC}\] (đối đỉnh)
Do đó \[\Delta AEC = \Delta DEB\] (c.g.c), suy ra \[AC = DB\] (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra \[BD = AC = CK\].
c) Xét \[\Delta AHC\] và \[\Delta KHE\] ta có \[AH = KH\], \[\widehat {AHE} = \widehat {KHE}\], \[HE\] là cạnh chung
Suy ra \[\Delta AHC = \Delta KHE\] (c.g.c) do đó \[\widehat {AEH} = \widehat {KEH}\] (2 góc tương ứng)
Suy ra \[EH\] là tia phân giác \[AEK\].
Vì \[\Delta AHE = \Delta KHE\] nên \[AE = KE\] mà \[AE = ED\]
Suy ra \[KE = ED\] do đó \[\Delta KED\] cân tại \[E\] nên \[\widehat {EKD} = \widehat {EDK}\].
\[\widehat {EDK} + \widehat {KED} = 90^\circ \] nên \[\widehat {EKD} = \frac{{180^\circ - \widehat {KED}}}{2}\]
Lại có \[\widehat {AKE} + \widehat {KED} = 180^\circ \] suy ra \[\widehat {AKE} = 180^\circ - \widehat {KED}\].
\[\widehat {AEH} + \widehat {HEK} = 180^\circ - \widehat {KED}\]
\[\widehat {HEK} = 180^\circ - \widehat {KED}\]
\[\widehat {HEK} = \frac{{180^\circ - \widehat {KED}}}{2}\] (4)
Từ (3) và (4) suy ra \[\widehat {HEK} = \widehat {ABC}\] mà chúng là 2 góc so le trong
Do đó \[HE{\rm{//}}KD\] hay \[BC{\rm{//}}KD\].
d) Xét \[\Delta KEN\] và \[\Delta DEN\] \[CE = ED\] (\[EN\] chung) \[KN = ND\] (\[N\] là trung điểm của \[KD\])
Suy ra \[\Delta KEN = \Delta DEN\] (c.c.c) nên \[\widehat {ENK} = \widehat {END}\] mà \[\widehat {ENK} + \widehat {END} = 180^\circ \].
Suy ra \[\widehat {ENC} = \widehat {END} = \frac{{180^\circ }}{2} = 90^\circ \] hay \[EN \bot KD\]. (*)
\[\Delta KBE = \Delta DCE\] suy ra \[BK = CD\] (2 cạnh tương ứng)
\[\Delta BKD = \Delta CDK\] (c.c.c) do đó \[\widehat {BDK} = \widehat {CKD}\] (2 góc tương ứng)
Suy ra \[\Delta KID\] cân tại \[I\] nên \[IK = ID\] xét \[\Delta KIN = \Delta DIN\] do đó \[\widehat {INK} - \widehat {IND}\].
Mà \[\widehat {INK} + \widehat {IND} = 180^\circ \] suy ra \[\widehat {INK} = \widehat {IND} = 90^\circ \] hay \[IN \bot KD\]. (**)
Từ (*) và (**) suy ra \(E,I,N\) thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.