Hai xe ô tô khởi hành cùng một lúc từ hai địa điểm \(A\) và \(B\), đi ngược chiều nhau trên cùng một tuyến đường. Đến điểm gặp nhau, xe thứ hai đi được quãng đường dài hơn xe thứ nhất là \(20{\rm{ km}}{\rm{.}}\) Biết rằng nếu đi hết quãng đường \(AB,\) xe thứ nhất đi hết 4 giờ 15 phút, xe thứ hai đi hết 3 giờ 45 phút. Tính độ dài quãng đường \(AB\).

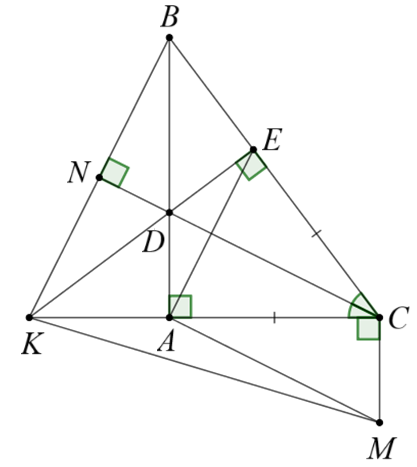
a) Vì \(CD\) là phân giác \(\widehat {BCA}\) suy ra \(\widehat {BCD} = \widehat {ACD}\).

Xét \(\Delta ACD\) và \(\Delta ECD\) có:

\(AC = AF\,;\,\,\widehat {BCD} = \widehat {ACD}\,;\,\,CD\) chung.

Do đó \(\Delta ACD = \Delta ECD\) (c.g.c).

Suy ra \(\widehat {CED} = \widehat {CAD} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\).

b) Vì \(AM\parallel CD\) suy ra \(\widehat {MAC} = \widehat {DCA}\) (hai góc so le trong)

Vì \(CM \bot CA\) nên \(\widehat {MCA} = 90^\circ \).

Xét \(\Delta CAD\) và \(\Delta ACM\) có:

\(\widehat {DAC} = \widehat {MCA} = 90^\circ \,;\,\,CA\) chung; \(\widehat {DCA} = \widehat {MAC}\).

Do đó \(\Delta CAD = \Delta ACM\) (g.c.g).

Suy ra (hai cạnh tương ứng).

c) Xét tam giác \(NBC\) và tam giác \(NKC\) có:

\(\widehat {BNC} = \widehat {KNC} = 90^\circ \,;\,\,NC\) chung; \(\widehat {BCN} = \widehat {CKN}\)

Suy ra \(\Delta NBC = \Delta NKC\,\)(g.c.g)

Do đó \(\widehat {NBC} = \widehat {NKC}\,;\,\,NB = NK\).

Xét tam giác \(NBD\) và tam giác \(NKD\) có:

\(NB = ND\,;\,\,\widehat {BND} = \widehat {KND}\,;\,\,ND\) chung.

Suy ra \(\Delta NBD = \Delta NKD\) (c.g.c).

Do đó, \(\widehat {NBD} = \widehat {NKD}\) (hai góc tương ứng)

d) Xét tam giác \(BKE\) và tam giác \(BKC\) có:

\[\widehat {BKE} = \widehat {BKA}\,;\,\,BK\] chung; \[\widehat {BKE} = \widehat {KBA}\].

Do đó \(\Delta BKE = \Delta BKC\) (g.c.g)

Suy ra \(\widehat {BEK} = \widehat {KAB} = 90^\circ \) (hai góc tương ứng)

Suy ra \(KE \bot BC\).

Mà \(DE \bot AC\).

Suy ra ba điểm \(K,\,D,\,E\) thẳng hàng.

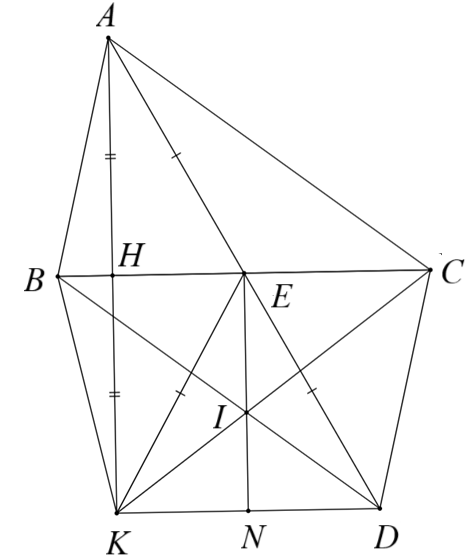
a) Xét \(\Delta AHC\) và \(\Delta KCH\) có

\(AH = HK\) (\(H\) là trung điểm của \(AK\))

\(\widehat {AHC} = \widehat {CHK}\) (\(AH \bot BC\))

\(CH\) là cạnh chung

Do đó \(\Delta AHC = \Delta KHC\) (cgc).

b) Vì \[\Delta AHC = \Delta KHC\] (chứng minh trên) do đó \[AC = CK\] (2 cạnh tương ứng)                            (1)

Xét \[\Delta AEC\] và \[\Delta DEB\] ta có :

\[AE = ED\] (\[E\] là trung điểm của \[AD\])

\[BE = CE\] (\[E\] là trung điểm của \[BE\]) \[\widehat {AEC} = \widehat {BEC}\] (đối đỉnh)

Do đó \[\Delta AEC = \Delta DEB\] (c.g.c), suy ra \[AC = DB\] (2 cạnh tương ứng)                  (2)

Từ (1) và (2) suy ra \[BD = AC = CK\].

c) Xét \[\Delta AHC\] và \[\Delta KHE\] ta có \[AH = KH\], \[\widehat {AHE} = \widehat {KHE}\], \[HE\] là cạnh chung

Suy ra \[\Delta AHC = \Delta KHE\] (c.g.c) do đó \[\widehat {AEH} = \widehat {KEH}\] (2 góc tương ứng)

Suy ra \[EH\] là tia phân giác \[AEK\].

Vì \[\Delta AHE = \Delta KHE\] nên \[AE = KE\] mà \[AE = ED\]

Suy ra \[KE = ED\] do đó \[\Delta KED\] cân tại \[E\] nên \[\widehat {EKD} = \widehat {EDK}\].

\[\widehat {EDK} + \widehat {KED} = 90^\circ \] nên \[\widehat {EKD} = \frac{{180^\circ - \widehat {KED}}}{2}\]

Lại có \[\widehat {AKE} + \widehat {KED} = 180^\circ \] suy ra \[\widehat {AKE} = 180^\circ - \widehat {KED}\].

\[\widehat {AEH} + \widehat {HEK} = 180^\circ - \widehat {KED}\]

\[\widehat {HEK} = 180^\circ - \widehat {KED}\]

\[\widehat {HEK} = \frac{{180^\circ - \widehat {KED}}}{2}\]                          (4)

Từ (3) và (4) suy ra \[\widehat {HEK} = \widehat {ABC}\] mà chúng là 2 góc so le trong

Do đó \[HE{\rm{//}}KD\] hay \[BC{\rm{//}}KD\].

d) Xét \[\Delta KEN\] và \[\Delta DEN\] \[CE = ED\] (\[EN\] chung) \[KN = ND\] (\[N\] là trung điểm của \[KD\])

Suy ra \[\Delta KEN = \Delta DEN\] (c.c.c) nên \[\widehat {ENK} = \widehat {END}\] mà \[\widehat {ENK} + \widehat {END} = 180^\circ \].

Suy ra \[\widehat {ENC} = \widehat {END} = \frac{{180^\circ }}{2} = 90^\circ \] hay \[EN \bot KD\].    (*)

\[\Delta KBE = \Delta DCE\] suy ra \[BK = CD\] (2 cạnh tương ứng)

\[\Delta BKD = \Delta CDK\] (c.c.c) do đó \[\widehat {BDK} = \widehat {CKD}\] (2 góc tương ứng)

Suy ra \[\Delta KID\] cân tại \[I\] nên \[IK = ID\] xét \[\Delta KIN = \Delta DIN\] do đó \[\widehat {INK} - \widehat {IND}\].

Mà \[\widehat {INK} + \widehat {IND} = 180^\circ \] suy ra \[\widehat {INK} = \widehat {IND} = 90^\circ \] hay \[IN \bot KD\].    (**)

Từ (*) và (**) suy ra \(E,I,N\) thẳng hàng.