Câu hỏi:

02/12/2025 39

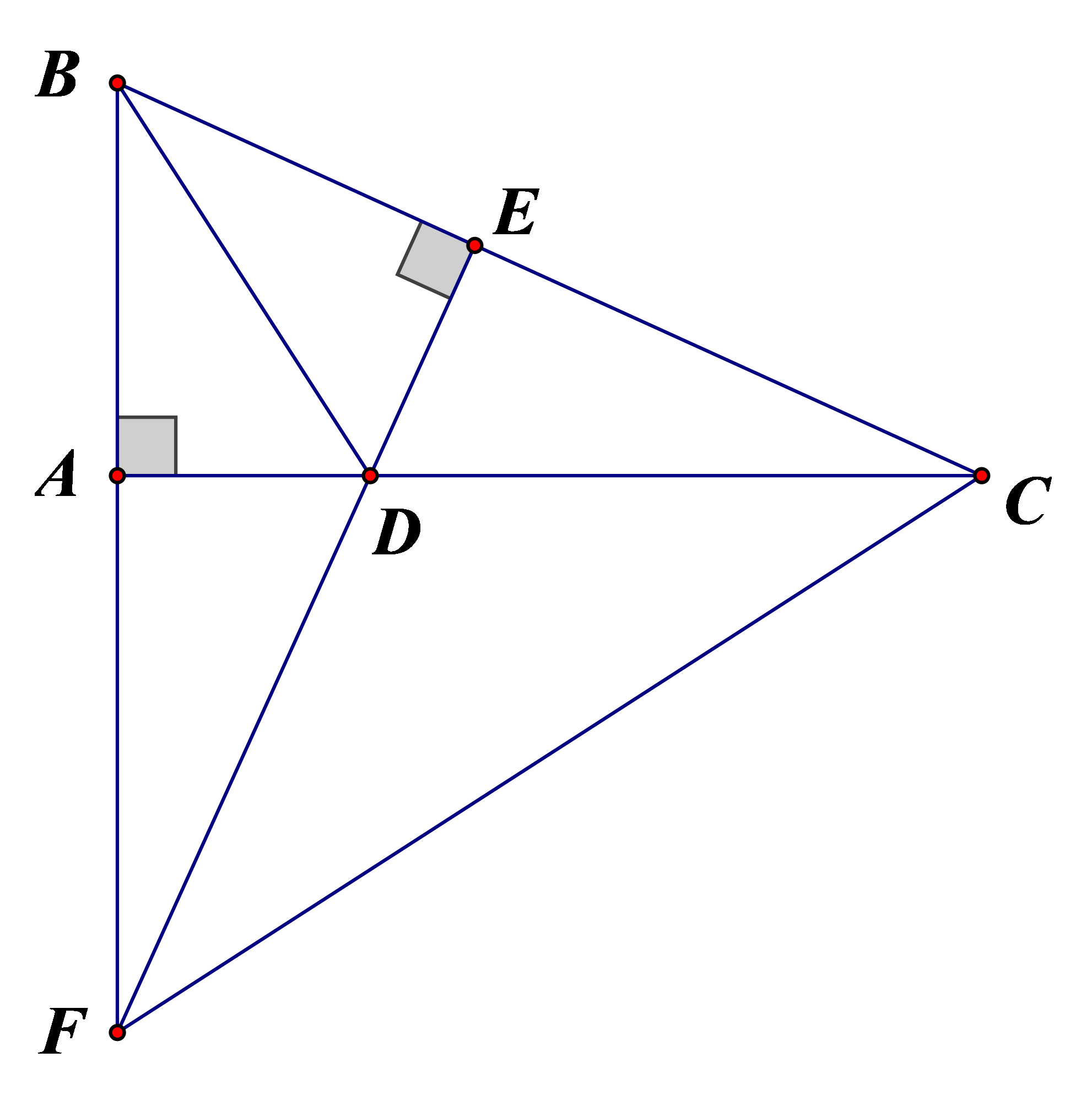
Cho $\Delta ABC$ vuông tại $A$. Trên cạnh $BC$ lấy điểm $E$ sao cho $BE = BA$, trên tia $BA$ lấy điểm $F$ sao cho $BF = BC$. Kẻ $BD$ là phân giác của $\widehat {ABC}\,\,\left( {D \in AC} \right)$. Chứng minh rằng:

a) $DE \bot BC$;

b) $AD < DC$;

c) $\Delta ADF = \Delta EDC.$

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập Giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

a) Xét $\Delta ABD$ và \[\Delta EBD\] có

$BE = BA$ (gt); $\widehat {ABD} = \widehat {EBD}$ (vì $BD$ là tia phân giác $\widehat {ABE}$); cạnh $BD$ chung.

Do đó $\Delta ABD = \Delta EBD$ (c.g.c).

Suy ra $\widehat {BAD} = \widehat {BED} = 90^\circ $ nên $DE \bot BC$.

b) Xét tam giác \[ECD\] vuông tại \[E\] nên cạnh huyền \[DC > DE\].

Mà \[DE = AD\] (vì $\Delta ABD = \Delta EBD$) nên $AD < DC.$

c) Ta có $BF = BC$ mà $BE = BA$ nên $AF = EC$.

Xét \[\Delta ADF\] và \[\Delta EDC\] có:

$AF = EC$ (cmt);

\[\widehat {DAF} = \widehat {DEC} = 90^\circ \];

$$AD = DE$ (vì \(\Delta ABD = \Del (ảnh 1)$

$AD = DE$ (vì $\Delta ABD = \Delta EBD$);

Do đó \[\Delta ADF = \Delta EDC\,\,{\rm{(c}}{\rm{.g}}{\rm{.c)}}\].

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác $ABC$, gọi $M$ là trung điểm của $BC$. Trên tia đối của tia $MA$ lấy điểm $D$ sao cho $MA = MD$. Chứng minh rằng:

a) $\Delta ABM = \Delta DCM$;

b) $AB\,{\rm{//}}\,CD$;

c) $AM < \frac{{AB + AC}}{2}$.

Xem đáp án

Lời giải

Hướng dẫn giải

a) Xét $\Delta ABM$ và $\Delta DCM$ có

$MA = MD$ (giả thiết)

$MB = MC$ (vì \[M\] là trung điểm)

$\widehat {ABM} = \widehat {CMD}$ (đối đỉnh)

Do đó $\Delta ABM = \Delta DCM$ (c.g.c)

b) Từ câu a: $\Delta ABM = \Delta DCM$.

Suy ra $\widehat {BAM} = \widehat {MDC}$.

Nên $AB\,{\rm{//}}\,CD$ (hai góc ở vị trí so le trong bằng nhau).

$Cho tam giác $ABC$, gọi $M$ là (ảnh 1)$

c) Xét bất đẳng thức trong tam giác \[ACD\] có $AD < AC + CD$.

Từ $\Delta ABM = \Delta DCM$ suy ra $AB = CD$ (hai cạnh tương ứng)

Do đó $AD < AC + AB$ nên $\frac{{AD}}{2} < \frac{{AB + AC}}{2}$.

Vậy $AM < \frac{{AB + AC}}{2}$.

Câu 2

Cho $a$, $b$, $c$ là ba số khác 0 thỏa mãn: $\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}$ (với giả thiết các tỉ số đều có nghĩa). Tính giá trị của biểu thức $M = \frac{{ab + bc + ca}}{{{a^2} + {b^2} + {c^2}}}$.

Xem đáp án

Lời giải

Hướng dẫn giải

Theo bài ra, ta có: $\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}$;

$\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{c + a}}{{ca}}$;

$\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c} = \frac{1}{c} + \frac{1}{a}$.

Suy ra $\frac{1}{a} = \frac{1}{c}$; $\frac{1}{b} = \frac{1}{a}$ hay $a = b = c$.

Với $a$, $b$, $c$ là ba số khác 0, thay $b = a$; $c = a$ vào biểu thức $M$, ta được:

$M = \frac{{ab + bc + ca}}{{{a^2} + {b^2} + {c^2}}} = \frac{{{a^2} + {a^2} + {a^2}}}{{{a^2} + {a^2} + {a^2}}} = \frac{{3{a^2}}}{{3{a^2}}} = 1$.

Vậy $M = 1$.

Câu 3