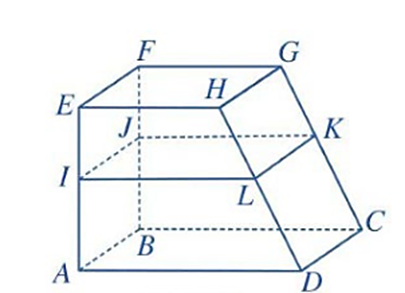
Mặt kệ để đồ bằng gỗ có mâm tầng dưới \(\left( {ABCD} \right)\) và mâm tầng trên \(\left( {EFGH} \right)\) song song với nhau. Bác thợ mộc đo được \(AE = 180\;{\rm{cm}}\)và muốn đóng thêm một mâm tầng giữa \(\left( {IJKL} \right)\) song song với hai mâm tầng trên và dưới sao cho khoảng cách \(EI = 60\;{\rm{cm}}\)(tham khảo hình vẽ). Hãy tính số \({{\rm{m}}^{\rm{2}}}\) gỗ cần dùng để làm mâm gỗ của tầng giữa biết rằng mâm gỗ dưới cùng là hình chữ nhật có diện tích \(7,2\;{{\rm{m}}^{\rm{2}}}\).

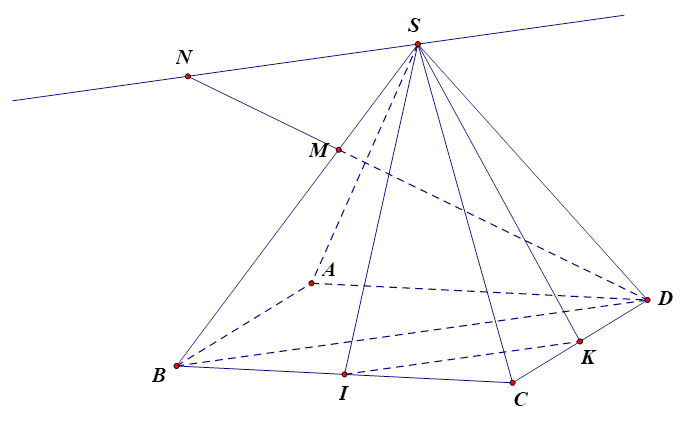
Ta có \(M\) là điểm trên cạnh \(SB\), \(\frac{{SM}}{{SB}} = \frac{1}{3}\) nên \(\frac{{MB}}{{MS}} = 2\).

\(IK//BD\) nên \(IK//\left( {SBD} \right)\). Suy ra \(\left( {SBD} \right) \cap \left( {SIK} \right) = Sx,Sx//IK//BD\).

Trong \(\left( {SBD} \right),DM \cap Sx = N\). \(N\)là giao điểm của \(DM\) và \(\left( {SIK} \right)\).

Trong \(\left( {SBD} \right)\), có \(Sx//BD\) nên hai tam giác \(SMN\) và \(BMD\) đồng dạng.

Do đó \(\frac{{MD}}{{MN}} = 2 \Rightarrow \frac{{ND}}{{NM}} = 3\).

Trả lời: 3.

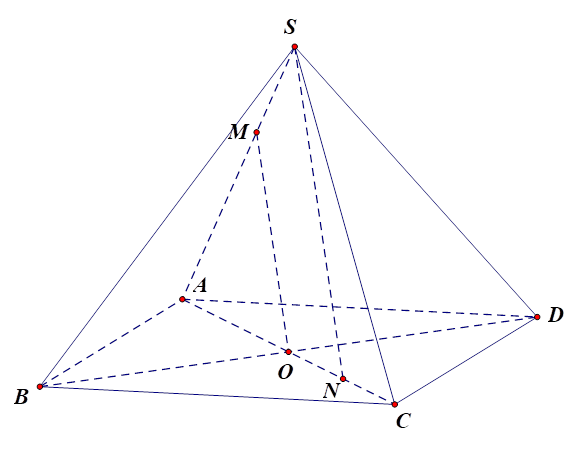
Trong mặt phẳng \(\left( {SAC} \right)\), kẻ \(SN//MO\left( {N \in AC} \right)\).

Khi đó \(N\) là hình chiếu của điểm \(S\) lên mặt phẳng \(\left( {ABCD} \right)\)theo phương chiếu \(MO\).

Vì \(MO//SN\) nên \(\frac{{AM}}{{MS}} = \frac{{AO}}{{ON}} = 2 \Rightarrow \frac{{OC}}{{ON}} = 2 \Rightarrow \frac{{CN}}{{CA}} = \frac{1}{4} = 0,25\).

Trả lời: 0,25.