a) Tính giá trị của biểu thức A:
A = 4,2 × 5,6 + 5,6 × 5,8 – 2,8
b) Tìm y, biết: y + \(\frac{1}{5}\)× y = \(1\frac{1}{2}\)+ 2 ̶ \(\frac{1}{2}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tính giá trị của biểu thức A:
A = 4,2 × 5,6 + 5,6 × 5,8 – 2,8
A = 5,6 × (4,2 + 5,8) – 2,8
A = 5,6 × 10 – 2,8
A = 56 – 2,8
A = 53,2
b) Tìm y, biết:
y + \(\frac{1}{5}\)× y = \(1\frac{1}{2}\)+ 2 ̶ \(\frac{1}{2}\)
y + 0,2 × y = \(\frac{3}{2}\)+ 2 ̶ \(\frac{1}{2}\)
y × (1 + 0,2) = \(\frac{3}{2}\) ̶ \(\frac{1}{2}\) + 2
y × 1,2 = 3
y = 3 : 1,2
y = 2,5
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
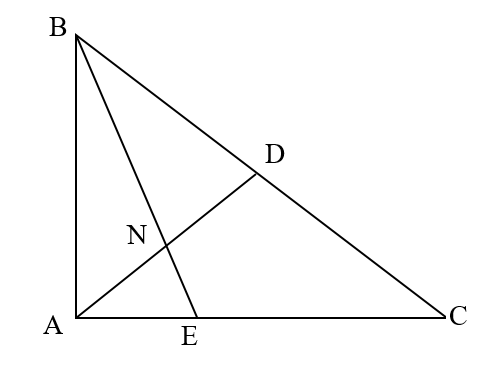
a) Diện tích tam giac ABC là: \(\frac{{12 \times 18}}{2} = 108\) (cm2)
Vì tam giác ADC và tam giác ABC có cùng chiều cao hạ từ A và cạnh đáy \(DC = \frac{1}{2}BC\) nên \({S_{ADC}} = \frac{1}{2} \times {S_{ABC}} = \frac{1}{2} \times 108 = 54\)(cm2)
Vì tam giác ADE và tam giác ADC có cùng chiều cao hạ từ D và cạnh đáy \(AE = \frac{1}{3}AC\) nên \({S_{ADE}} = \frac{1}{3} \times {S_{ADC}} = \frac{1}{3} \times 54 = 18\)(cm2)
b) Ta có \(AE = \frac{1}{3} \times AC = \frac{1}{3} \times 18 = 6\) (cm)
Diện tích tam giác ABE là: \(\frac{{12 \times 6}}{2} = 36\)(cm2)
Vì \(AE = \frac{1}{3}AC\) nên \(EC = \frac{2}{3}AC\) nên \({S_{DEC}} = \frac{2}{3} \times {S_{ADC}} = \frac{2}{3} \times 54 = 36\) (cm2)
(Hai tam giác chung chiều cao hạ từ D và cạnh đáy \(EC = \frac{2}{3}AC\))
Mặt khác tổng diện tích 3 tam giác ABE, BDE, DEC bằng diện tích tam giác ABC
Nên \({S_{DBE}} = {S_{ABC}} - {S_{ABE}} - {S_{DEC}}\, = 108 - 36 - 36 = 36\)(cm2)
Vậy \({S_{ABE}} = {S_{DBE}}\)
Đáp số: a) \({S_{ADE}} = 18\) cm2
b) \({S_{ABE}} = {S_{DBE}}\)
Lời giải
a) Các màu bi lặp lại theo chu kỳ có thứ tự: xanh, đỏ, tím, vàng
Do đó chu kỳ này gồm 4 màu
Mà 2 014 chia cho 4 được 503 dư 2, nên khi trong hộp có 2 014 viên bi thì sẽ có 503 chu kỳ như trên và dư ra 2 viên theo thứ tự là xanh, đỏ
Vậy số viên bi xanh là: 503 + 1 = 504 (viên)
Số viên bi đỏ là: 503 + 1 = 504 (viên)
Số viên bi tím là: 503 (viên)
Số viên bi vàng là: 503 (viên)
b) Để đảm bảo có đủ 4 màu, cần lấy tất cả bi của 3 màu có số lượng lớn nhất và thêm 1 viên của màu còn lại:
504 (xanh) + 504 (đỏ) + 503 (tím) + 1 (vàng) = 1 512 (viên)
Đáp số: a) xanh: 504 viên; đỏ: 504 viên; tím: 503 viên; vàng: 503 viên
b) lấy ít nhất 1 512 viên
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập