Cho vào hộp lần lượt các viên bi: xanh, đỏ, tím, vàng rồi lại tiếp tục xanh, đỏ, tím, vàng, … cho đến khi trong hộp có 2 014 viên bi.
a) Tính số viên bi mỗi loại.
b) Không nhìn vào hộp, em cần lấy ít nhất bao nhiêu viên bi để chắc chắn trong số bi lấy ra có đủ bốn màu: xanh, đỏ, tím, vàng?
Cho vào hộp lần lượt các viên bi: xanh, đỏ, tím, vàng rồi lại tiếp tục xanh, đỏ, tím, vàng, … cho đến khi trong hộp có 2 014 viên bi.
a) Tính số viên bi mỗi loại.
b) Không nhìn vào hộp, em cần lấy ít nhất bao nhiêu viên bi để chắc chắn trong số bi lấy ra có đủ bốn màu: xanh, đỏ, tím, vàng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Các màu bi lặp lại theo chu kỳ có thứ tự: xanh, đỏ, tím, vàng
Do đó chu kỳ này gồm 4 màu
Mà 2 014 chia cho 4 được 503 dư 2, nên khi trong hộp có 2 014 viên bi thì sẽ có 503 chu kỳ như trên và dư ra 2 viên theo thứ tự là xanh, đỏ
Vậy số viên bi xanh là: 503 + 1 = 504 (viên)
Số viên bi đỏ là: 503 + 1 = 504 (viên)
Số viên bi tím là: 503 (viên)
Số viên bi vàng là: 503 (viên)
b) Để đảm bảo có đủ 4 màu, cần lấy tất cả bi của 3 màu có số lượng lớn nhất và thêm 1 viên của màu còn lại:
504 (xanh) + 504 (đỏ) + 503 (tím) + 1 (vàng) = 1 512 (viên)
Đáp số: a) xanh: 504 viên; đỏ: 504 viên; tím: 503 viên; vàng: 503 viên
b) lấy ít nhất 1 512 viên
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
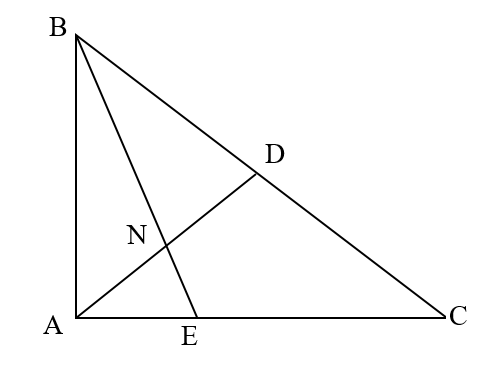
a) Diện tích tam giac ABC là: \(\frac{{12 \times 18}}{2} = 108\) (cm2)
Vì tam giác ADC và tam giác ABC có cùng chiều cao hạ từ A và cạnh đáy \(DC = \frac{1}{2}BC\) nên \({S_{ADC}} = \frac{1}{2} \times {S_{ABC}} = \frac{1}{2} \times 108 = 54\)(cm2)
Vì tam giác ADE và tam giác ADC có cùng chiều cao hạ từ D và cạnh đáy \(AE = \frac{1}{3}AC\) nên \({S_{ADE}} = \frac{1}{3} \times {S_{ADC}} = \frac{1}{3} \times 54 = 18\)(cm2)
b) Ta có \(AE = \frac{1}{3} \times AC = \frac{1}{3} \times 18 = 6\) (cm)
Diện tích tam giác ABE là: \(\frac{{12 \times 6}}{2} = 36\)(cm2)
Vì \(AE = \frac{1}{3}AC\) nên \(EC = \frac{2}{3}AC\) nên \({S_{DEC}} = \frac{2}{3} \times {S_{ADC}} = \frac{2}{3} \times 54 = 36\) (cm2)
(Hai tam giác chung chiều cao hạ từ D và cạnh đáy \(EC = \frac{2}{3}AC\))
Mặt khác tổng diện tích 3 tam giác ABE, BDE, DEC bằng diện tích tam giác ABC
Nên \({S_{DBE}} = {S_{ABC}} - {S_{ABE}} - {S_{DEC}}\, = 108 - 36 - 36 = 36\)(cm2)
Vậy \({S_{ABE}} = {S_{DBE}}\)
Đáp số: a) \({S_{ADE}} = 18\) cm2
b) \({S_{ABE}} = {S_{DBE}}\)
Lời giải
a) Số đồng chí có chiều cao 180 cm là:
120 × 40 : 100 = 48 (đồng chí)
Tỉ số của số đồng chí có chiều cao 180 cm và số đồng chí tham gia buổi diễu binh là:
\(\frac{{48}}{{120}} = \frac{2}{5}\)
b) Tổng số đồng chí có chiều cao 183 cm và 185 cm là:
120 ̶ 48 = 72 (đồng chí)
Tỉ số số đồng chí có chiều cao 183 cm và số đồng chí có chiều cao 185 cm là: \(\frac{3}{5}\)
Tổng số phần bằng nhau là: 3 + 5 = 8 (phần)
Số đồng chí có chiều cao 183 cm là:
(72 : 8) × 3 = 27 (đồng chí)
Số đồng chí có chiều cao 185 cm là:
72 ̶ 27 = 45 (đồng chí)
Đáp số: a) \(\frac{2}{5}\)
b) chiều cao 183 cm: 27 đồng chí; chiều cao 185 cm: 45 đồng chí
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập