Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện ra số lượng vi khuẩn tăng thêm 25% sau hai ngày.
a) Công thức \(P\left( t \right) = {P_0} \cdot {a^t}\) cho phép tính số lượng vi khuẩn mẻ nuôi cấy sau \(t\) ngày kể từ thời điểm ban đầu. Xác định các tham số \({P_0}\) và \(a\left( {a > 0} \right)\) (làm tròn đến hàng phần trăm).
Lấy kết quả đã làm tròn ở ý a để làm ý b và c.
b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu (làm tròn đến hàng phần trăm).
c) Sau bao nhiêu ngày thì số lượng vi khuẩn bằng gấp đôi số lượng ban đầu (làm tròn kết quả đến hàng phần chục)?
Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện ra số lượng vi khuẩn tăng thêm 25% sau hai ngày.
a) Công thức \(P\left( t \right) = {P_0} \cdot {a^t}\) cho phép tính số lượng vi khuẩn mẻ nuôi cấy sau \(t\) ngày kể từ thời điểm ban đầu. Xác định các tham số \({P_0}\) và \(a\left( {a > 0} \right)\) (làm tròn đến hàng phần trăm).
Lấy kết quả đã làm tròn ở ý a để làm ý b và c.
b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu (làm tròn đến hàng phần trăm).
c) Sau bao nhiêu ngày thì số lượng vi khuẩn bằng gấp đôi số lượng ban đầu (làm tròn kết quả đến hàng phần chục)?
Câu hỏi trong đề: Bài tập ôn tập Toán 11 Kết nối tri thức Chương 6 có đáp án !!
Quảng cáo
Trả lời:
a) Ban đầu có 1000 vi khuẩn nên \({P_0} = 1000\).
Sau hai ngày, số lượng vi khuẩn là \(P = 125\% \cdot 1000 = 1250\).
Ta có \(P\left( 2 \right) = 1000 \cdot {a^2} \Leftrightarrow 1250 = 1000 \cdot {a^2} \Leftrightarrow {a^2} = \frac{5}{4} \Rightarrow a \approx 1,12\).
b) Số lượng vi khuẩn sau 5 ngày là \(P\left( 5 \right) = 1000 \cdot {\left( {1,12} \right)^5} \approx 1800\).
c) Với \(P\left( t \right) = 2{P_0} \Leftrightarrow 2{P_0} = {P_0} \cdot {1,12^t} \Leftrightarrow {1,12^t} = 2 \Leftrightarrow t = {\log _{1,12}}2 \approx 6,1\) ngày.
Vậy sau 6,1 ngày thì số lượng vi khuẩn bằng gấp đôi số lượng ban đầu.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) Tập xác định của hàm số \(D = \left[ { - \frac{3}{2}; + \infty } \right)\).
b) Nghiệm của phương trình \(f\left( x \right) = 1\) là \(x = 0\).
c) Tập nghiệm của bất phương trình \(f\left( x \right) < 2\) có đúng 3 số nguyên.
Lời giải
a) Điều kiện \(2x + 3 > 0 \Leftrightarrow x > - \frac{3}{2}\).
Tập xác định của hàm số \(D = \left( { - \frac{3}{2}; + \infty } \right)\).
b) \(f\left( x \right) = 1\) \( \Leftrightarrow {\log _3}\left( {2x + 3} \right) = 1\)\( \Leftrightarrow 2x + 3 = 3\)\( \Leftrightarrow x = 0\).
c) Ta có \(f\left( x \right) < 2 \Leftrightarrow {\log _3}\left( {2x + 3} \right) < 2\)\( \Leftrightarrow 2x + 3 < 9\)\( \Leftrightarrow x < 3\).
Kết hợp với điều kiện ta có \(S = \left( { - \frac{3}{2};3} \right)\), mà \(x \in \mathbb{Z}\) nên \(x \in \left\{ { - 1;0;1;2} \right\}\).
Vậy có 4 giá trị nguyên của \(x\) để \(f\left( x \right) < 2\).
d) Vì hàm số \(y = f\left( x \right) = {\log _3}\left( {2x + 3} \right)\) đồng biến trên \(\left( { - \frac{3}{2}; + \infty } \right)\) nên \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( 0 \right) = 1;\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( 3 \right) = 2\).
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên \(\left[ {0;3} \right]\) là 3.
Đáp án: a) Sai; b) Đúng; c) Sai; d) Đúng.
Câu 2
A. \(\frac{{13}}{6}\).
Lời giải
Ta có \(\frac{{\sqrt {2\sqrt[3]{4}} }}{{{{16}^{0,75}}}}\)\( = \frac{{\sqrt {2 \cdot {2^{\frac{2}{3}}}} }}{{{2^{4 \cdot }}^{0,75}}}\)\( = \frac{{\sqrt {{2^{\frac{5}{3}}}} }}{{{2^3}}}\)\[ = \frac{{{2^{\frac{5}{6}}}}}{{{2^3}}}\]\[ = {2^{\frac{{ - 13}}{6}}}\]. Suy ra \(m = - \frac{{13}}{6}\). Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
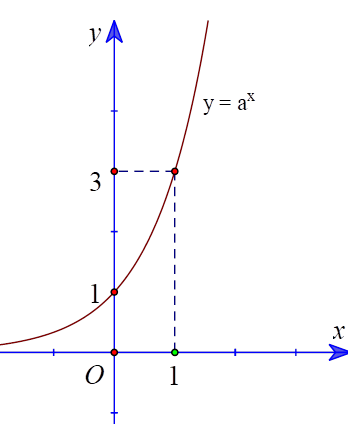
Câu 4
a) Đồ thị hàm số đã cho cắt đường thẳng \(y = - x + 1\) tại điểm có hoành độ dương.
b) Hàm số cho bởi công thức \(y = {3^x}\).
c) Hàm số đã cho nghịch biến trên khoảng (0; 1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \({\log _{15}}4 = \frac{{a + b}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.