Một ô tô khởi hành từ A với vận tốc 60 km/h và dự định tới B sau 3 giờ. Thực tế sau khi đi được 1 giờ 15 phút, xe bị hỏng nên phải dừng lại để sửa hết 15 phút. Hỏi muốn đến B đúng thời gian dự định thì trên đoạn đường còn lại ô tô phải đi với vận tốc là bao nhiêu km/h?

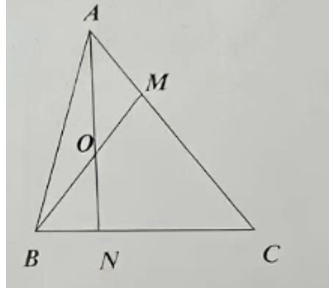
a) Ta có AM = \(\frac{1}{2}\)MC nên AM = \(\frac{1}{3}\)AC

\(\frac{{{S_{ABM}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AC}} = \frac{1}{3}\) (Hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và đáy AM = \(\frac{1}{3}\)AC)

Suy ra S_ABM = \(\frac{1}{3}\)× S_ABC = \(\frac{1}{3}\)× 60 = 20 (cm²)

\(\frac{{{S_{ABO}}}}{{{S_{ABM}}}} = \frac{{BO}}{{BM}} = \frac{1}{2}\) (Hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BM và đáy BO = \(\frac{1}{2}\)BM)

Suy ra S_ABO = \(\frac{1}{2}\)× S_ABM = \(\frac{1}{2}\)× 20 = 10 (cm²)

b) Nối O với C

Ta có S_ABO = S_AOM (Hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BM và đáy BO = OM)

S_AOM = \(\frac{1}{3}\)× S_AOC  (Hai tam giác có chung chiều cao hạ từ đỉnh O xuống đáy AC và đáy AM = \(\frac{1}{3}\)AC)

Suy ra S_ABO = \(\frac{1}{3}\)S_AOC

Suy ra chiều cao hạ từ B xuống đáy AN = \(\frac{1}{3}\) chiều cao hạ từ C xuống đáy AN

Suy ra S_ABN = \(\frac{1}{3}\)S_ACN (Hai tam giác chung đáy AN)

Vậy BN = \(\frac{1}{3}\)NC (chung chiều cao hạ từ A xuống đáy BC)

= \[\frac{{17}}{9}\]   × ( 8 × \[\frac{{34}}{9}\]) - \[\frac{9}{5}\]

= \[\frac{{17}}{9}\] × \[\frac{{36}}{{17}}\] - \[\frac{9}{5}\]

= 4 - \[\frac{9}{5}\]

= \[\frac{{11}}{9}\]