Một trường tiểu học có 220 học sinh khối 4 và 180 học sinh khối 5. Cuối năm học có 30% số học sinh khối 4 đạt danh hiệu Học sinh xuất sắc và 25% số học sinh khối 5 đạt danh hiệu Học sinh xuất sắc. Hỏi cả hai khối 4 và 5, tỉ lệ học sinh đạt danh hiệu Học sinh xuất sắc là bao nhiêu phần trăm?

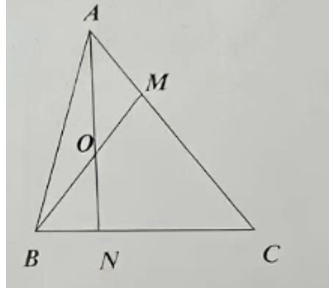
a) Ta có AM = \(\frac{1}{2}\)MC nên AM = \(\frac{1}{3}\)AC

\(\frac{{{S_{ABM}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AC}} = \frac{1}{3}\) (Hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và đáy AM = \(\frac{1}{3}\)AC)

Suy ra S_ABM = \(\frac{1}{3}\)× S_ABC = \(\frac{1}{3}\)× 60 = 20 (cm²)

\(\frac{{{S_{ABO}}}}{{{S_{ABM}}}} = \frac{{BO}}{{BM}} = \frac{1}{2}\) (Hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BM và đáy BO = \(\frac{1}{2}\)BM)

Suy ra S_ABO = \(\frac{1}{2}\)× S_ABM = \(\frac{1}{2}\)× 20 = 10 (cm²)

b) Nối O với C

Ta có S_ABO = S_AOM (Hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BM và đáy BO = OM)

S_AOM = \(\frac{1}{3}\)× S_AOC  (Hai tam giác có chung chiều cao hạ từ đỉnh O xuống đáy AC và đáy AM = \(\frac{1}{3}\)AC)

Suy ra S_ABO = \(\frac{1}{3}\)S_AOC

Suy ra chiều cao hạ từ B xuống đáy AN = \(\frac{1}{3}\) chiều cao hạ từ C xuống đáy AN

Suy ra S_ABN = \(\frac{1}{3}\)S_ACN (Hai tam giác chung đáy AN)

Vậy BN = \(\frac{1}{3}\)NC (chung chiều cao hạ từ A xuống đáy BC)

Gọi số tuổi của ông nội hiện nay là ab (a khác 0) thì số tuổi của bố là ba ( b khác 0)

Gọi tuổi Nam hiện nay là c (c khác 0)

Theo đề bài tổng số tuổi của ông nội, bố và Nam là 144 tuổi nên:

Ab + ba + c = 144

a × 10 + b + b × 10 + a + c = 144

a × 11 + b × 11 + c = 144

11 × (a + b) + c = 144             (1)

Ta có: Cộng tất cả các chữ số trong tuổi của ông và bố thì được một số gấp đôi tuổi Nam.

Suy ra (a + b + b + a) = 2 × c

            2 × (a + b) = 2 × c

                    a + b = c

Thay vào (1) ta có 11 × c + c = 144 hay 12 × c = 144

Suy ra c = 144 : 12 = 12

Tuổi Nam sau 3 năm nữa là 12 + 3 = 15 (tuổi)

Đáp số: 15 tuổi