Cho tam giác \[ABC\]vuông tại \[A\] có diện tích bằng \[18{m^2}\].
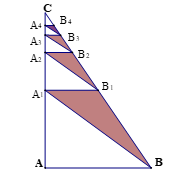
Gọi \[{A_1},{A_2},{A_3},{A_4},....\]lần lượt là trung điểm của các đoạn \[AC,{A_1}C,{A_2}C,{A_3}C,.....\].
Nối \[B{A_1}\], kẻ \[{A_1}{B_1}\]song song\[AB\]ta được tam giác \[B{A_1}{B_1}\];
nối \[{B_1}{A_2}\], kẻ \[{A_2}{B_2}\]song song\[AB\]ta được tam giác \[{B_1}{A_2}{B_2}\];
nối \[{B_2}{A_3}\], kẻ \[{A_3}{B_3}\]song song\[AB\]ta được tam giác \[{B_2}{A_3}{B_3}\]
(như hình vẽ). Và cứ tiếp tục như vậy ta được nhiều tam giác như thế.
Tính tổng diện tích của các tam giác này.
( Khi làm bài này học sinh có thể không vẽ lại hình)
Cho tam giác \[ABC\]vuông tại \[A\] có diện tích bằng \[18{m^2}\].
Gọi \[{A_1},{A_2},{A_3},{A_4},....\]lần lượt là trung điểm của các đoạn \[AC,{A_1}C,{A_2}C,{A_3}C,.....\].
Nối \[B{A_1}\], kẻ \[{A_1}{B_1}\]song song\[AB\]ta được tam giác \[B{A_1}{B_1}\];
nối \[{B_1}{A_2}\], kẻ \[{A_2}{B_2}\]song song\[AB\]ta được tam giác \[{B_1}{A_2}{B_2}\];
nối \[{B_2}{A_3}\], kẻ \[{A_3}{B_3}\]song song\[AB\]ta được tam giác \[{B_2}{A_3}{B_3}\]
(như hình vẽ). Và cứ tiếp tục như vậy ta được nhiều tam giác như thế.
Tính tổng diện tích của các tam giác này.
( Khi làm bài này học sinh có thể không vẽ lại hình)
Quảng cáo
Trả lời:
Giải bởi Vietjack
\[{S_{\Delta AB{A_1}}} = \frac{1}{2}{S_{\Delta ABC}}\] , \[{S_{\Delta {A_1}{B_1}C}} = \frac{1}{4}{S_{\Delta ABC}}\]\[ \Rightarrow {S_{\Delta B{A_1}}}_{{B_1}} = \frac{1}{4}{S_{\Delta ABC}} = \frac{9}{2}\]
\[\Delta {B_1}{A_2}{B_2}\]đồng dạng \[\Delta B{A_1}{B_1}\] tỉ số \[1/2\]\[{S_{\Delta {B_1}{A_2}{B_2}}} = \frac{1}{4}{S_{\Delta B{A_1}{B_1}}} = \frac{1}{{16}}{S_{\Delta ABC}} = \frac{9}{8}\]…..
Ta có CSN \[{u_1} = \frac{9}{2},q = \frac{1}{4}\]
Tổng diện tích các tam giác tô đậm: \[{S_1} = \frac{{{u_1}}}{{1 - q}} = 6{m^2}\]
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Câu 2
Lời giải
Chọn C
\[\sin x = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{4} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{{3\pi }}{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập