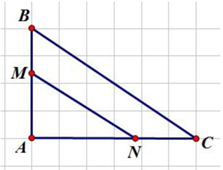
Một hình tam giác ABC có D là điểm chính giữa của BC, E là điểm chính giữa của CA, AD cắt BE ở G. Hãy chứng tỏ AG gấp đôi GD.
Một hình tam giác ABC có D là điểm chính giữa của BC, E là điểm chính giữa của CA, AD cắt BE ở G. Hãy chứng tỏ AG gấp đôi GD.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng Dẫn Giải
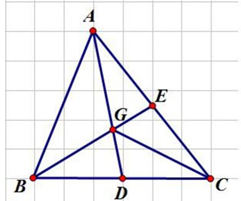
Nối C với G.
Ta có: \({S_{BCE}} = {S_{ACD}}\) (Vì cùng bằng \(\frac{1}{2}{S_{ABC}}\))
Mà: \({S_{BCE}} = {S_{GBD}} + {S_{CDGE}}\) và \({S_{ACD}} = {S_{GAE}} + {S_{CDGE}}\)
\( \Rightarrow {S_{GBD}} = {S_{GAE}} = \frac{1}{2}{S_{GAC}}\) (1)
Cũng có: \({S_{GBD}} = {S_{GCD}}\) (chung chiều cao hạ từ G, đáy \(BD = CD\)) (2)
Từ (1) và (2) suy ra: \({S_{GCD}} = \frac{1}{2}{S_{GAC}}\) mà hai tam giác này chung chiều cao hạ từ C nên: \(GD = \frac{1}{2}GA\) hay GA gấp đôi GD. (đpcm)
Đáp Số: gấp đôi.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng Dẫn Giải
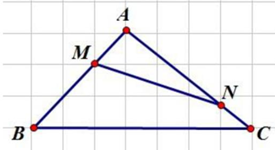
Vì \(MN//BC \Rightarrow MNBC\) là hình thang.
Nối BN, CM
\({S_{BCM}} = \frac{1}{3}{S_{ABC}}\) (\(BM = 30 - 20 = 10{\rm{ cm, }}\frac{{BM}}{{AB}} = \frac{{10}}{{30}} = \frac{1}{3}\), chung chiều cao hạ từ C)
\({S_{BMC}} = {S_{BNC}}\) (chung đáy BC, chiều cao là chiều cao hình thang MNBC)
Mà \({S_{ABC}} = 30 \times 45:2 = 675{\rm{ c}}{{\rm{m}}^2}\)
\( \Rightarrow {S_{BNC}} = 675 \times \frac{1}{3} = 225{\rm{ c}}{{\rm{m}}^2}\)
Độ dài NC = \(225 \times 2:30 = 15{\rm{ cm}}\)
Độ dài AN = \(45 - 15 = 30{\rm{ cm}}\)
\({S_{AMN}} = 30 \times 20:2 = 300{\rm{ c}}{{\rm{m}}^2}\)
Đáp Số: \(300{\rm{ c}}{{\rm{m}}^2}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng Dẫn Giải
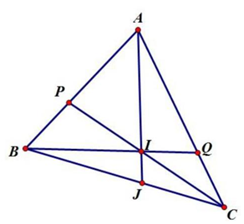
Vì \(BP = \frac{1}{2}PA;CQ = \frac{1}{3}QA\) nên có:
\({S_{IAP}} = 2 \times {S_{IBP}}\); \({S_{IAQ}} = 3 \times {S_{ICQ}}\);
\({S_{IAP}} + {S_{IAQ}} + {S_{IBQ}} = \frac{2}{3} \times {S_{ABC}}\)
\({S_{IBP}} + {S_{IAP}} + {S_{IAQ}} = \frac{3}{4} \times {S_{ABC}}\)
Từ đó có được:
\({S_{IBP}} = \frac{1}{6} \times {S_{ABC}};{S_{IAP}} = \frac{1}{3} \times {S_{ABC}};{S_{IAQ}} = \frac{1}{4} \times {S_{ABC}};{S_{ICQ}} = \frac{1}{{12}} \times {S_{ABC}}\)
Vậy: \(\frac{{BJ}}{{JC}} = \frac{{{S_{IBJ}}}}{{{S_{ICJ}}}} = \frac{{{S_{IAP}} + {S_{IBP}} + {S_{IBJ}}}}{{{S_{IAQ}} + {S_{ICQ}} + {S_{ICJ}}}} = \frac{{{S_{IAP}} + {S_{IBP}}}}{{{S_{IAQ}} + {S_{ICQ}}}} = \frac{{\frac{1}{3} \times {S_{ABC}} + \frac{1}{6} \times {S_{ABC}}}}{{\frac{1}{4} \times {S_{ABC}} + \frac{1}{{12}} \times {S_{ABC}}}} = \frac{{\frac{1}{2}}}{{\frac{1}{3}}} = \frac{3}{2}\)
Đáp Số: \(\frac{{BJ}}{{JC}} = \frac{3}{2}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập