Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật có \(AB = 1,AD = 2\). Tam giác \(SAD\) đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBD} \right)\) (làm tròn kết quả đến hàng phần trăm).
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật có \(AB = 1,AD = 2\). Tam giác \(SAD\) đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBD} \right)\) (làm tròn kết quả đến hàng phần trăm).
Câu hỏi trong đề: Đề kiểm tra Toán 11 Kết nối tri thức Chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
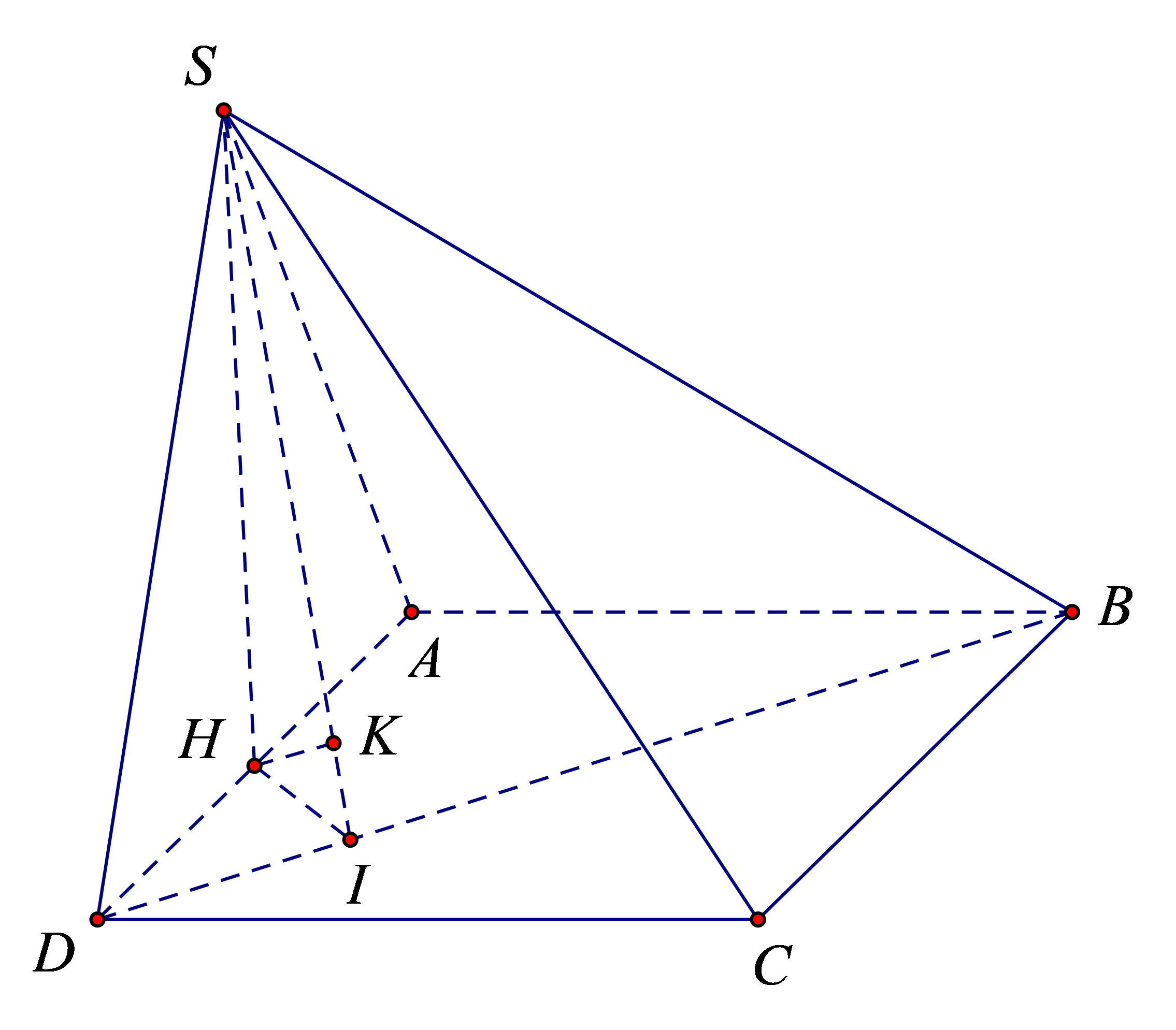
Gọi \(H\) là trung điểm của \(AD\).
Vì \(\Delta SAD\) đều nên \(SH \bot AD\) mà \(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\) nên \(SH \bot \left( {ABCD} \right)\).
Hạ \(HI \bot BD\) và \(SH \bot BD\left( {SH \bot \left( {ABCD} \right)} \right)\) nên \(BD \bot \left( {SHI} \right)\).
Hạ \(HK \bot SI\) và \(HK \bot BD\left( {BD \bot \left( {SHI} \right)} \right)\) nên \(HK \bot \left( {SBD} \right)\).
Suy ra \(d\left( {H,\left( {SBD} \right)} \right) = HK\).
Có \(\Delta DIH\) đồng dạng \(DAB\) nên \(\frac{{DH}}{{DB}} = \frac{{IH}}{{AB}} \Rightarrow \frac{{IH}}{{AB}} = \frac{1}{{\sqrt 5 }} \Rightarrow IH = \frac{{\sqrt 5 }}{5}\).
Có \(\Delta SAD\) đều cạnh bằng 2 nên \(SH = \frac{{2\sqrt 3 }}{2} = \sqrt 3 \).
Xét \(\Delta SHI\) vuông tại \(H\), có \(\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{1}{3} + 5 = \frac{{16}}{3} \Rightarrow HK = \frac{{\sqrt 3 }}{4}\).
Lại có \(\frac{{d\left( {A,\left( {SBD} \right)} \right)}}{{d\left( {H,\left( {SBD} \right)} \right)}} = \frac{{AD}}{{HD}} = 2 \Rightarrow d\left( {A,\left( {SBD} \right)} \right) = 2d\left( {H,\left( {SBD} \right)} \right) = \frac{{2\sqrt 3 }}{4} \approx 0,87\).
Trả lời: 0,87.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
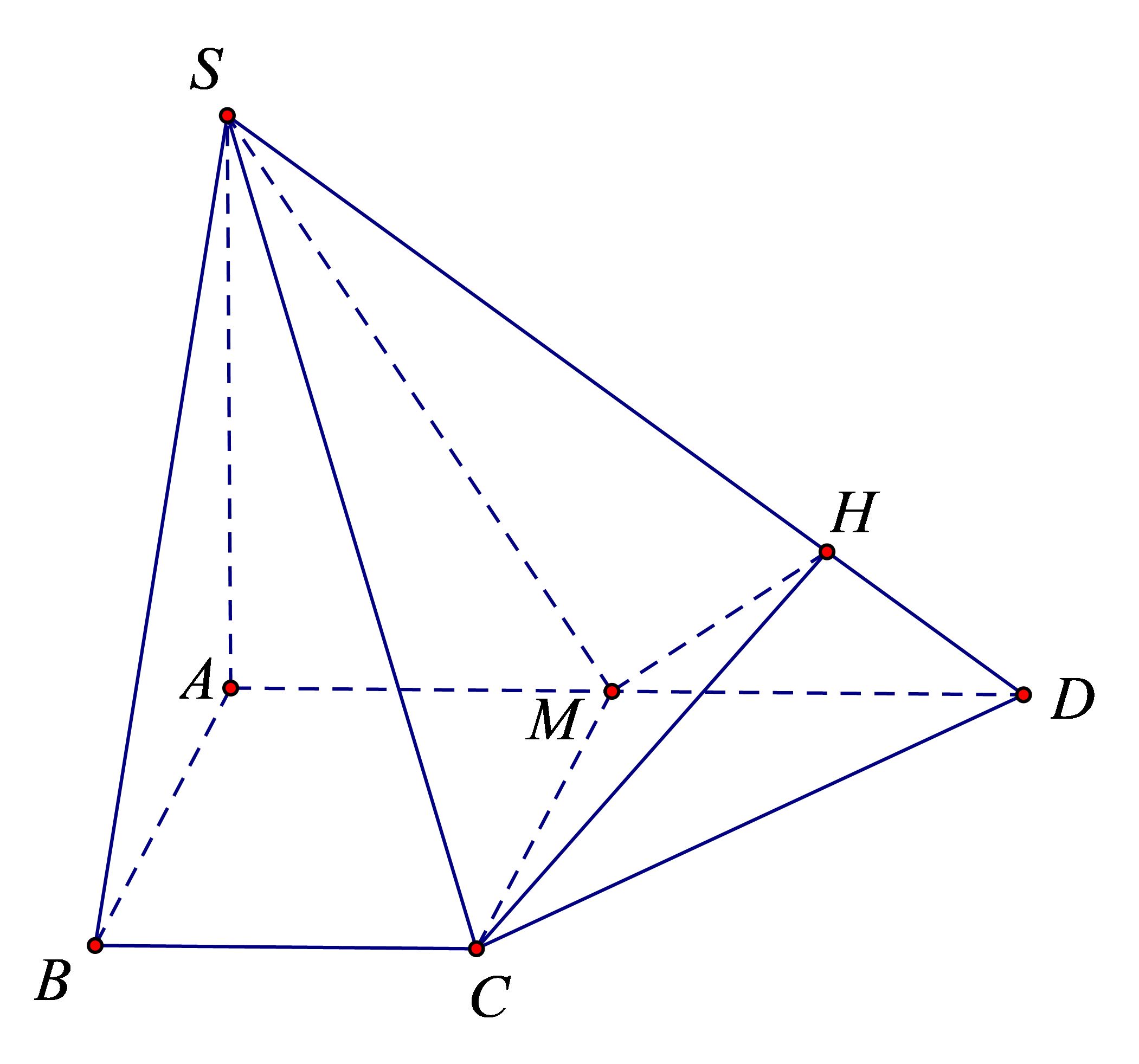
Gọi \(M\) là trung điểm của \(AD\). Khi đó \(ABCM\) là hình vuông.
Hạ \(MH \bot SD\).
Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot CM\) mà \(CM \bot AD\) nên \(CM \bot \left( {SAD} \right)\). Suy ra \(CM \bot SD\).
Lại có \(MH \bot SD\) nên \(SD \bot \left( {MHC} \right)\). Suy ra \(CH \bot SD\).
Do đó \(\left[ {A,SD,C} \right] = \left[ {M,SD,C} \right] = \widehat {MHC}\).
Xét \(\Delta SAD\) vuông tại \(A\), có \(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 2 }}{{2a}} = \frac{{\sqrt 2 }}{2}\).
Suy ra \(\sin \widehat {SDA} = \frac{{\sqrt 3 }}{3}\).
Xét \(\Delta MHD\) vuông tại \(H\), có \(\sin \widehat {SDA} = \frac{{MH}}{{MD}} \Rightarrow MH = \frac{{a\sqrt 3 }}{3}\).
Vì \(CM \bot \left( {SAD} \right)\) nên \(CM \bot MH\). Do đó \(\Delta CMH\) vuông tại \(M\).
Có \(CH = \sqrt {C{M^2} + M{H^2}} = \sqrt {{a^2} + \frac{{3{a^2}}}{9}} = \frac{{2a\sqrt 3 }}{3}\).
\(\cos \widehat {MHC} = \frac{{MH}}{{CH}} = \frac{{a\sqrt 3 }}{3}:\frac{{2a\sqrt 3 }}{3} = \frac{1}{2} = 0,5\).
Trả lời: 0,5.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
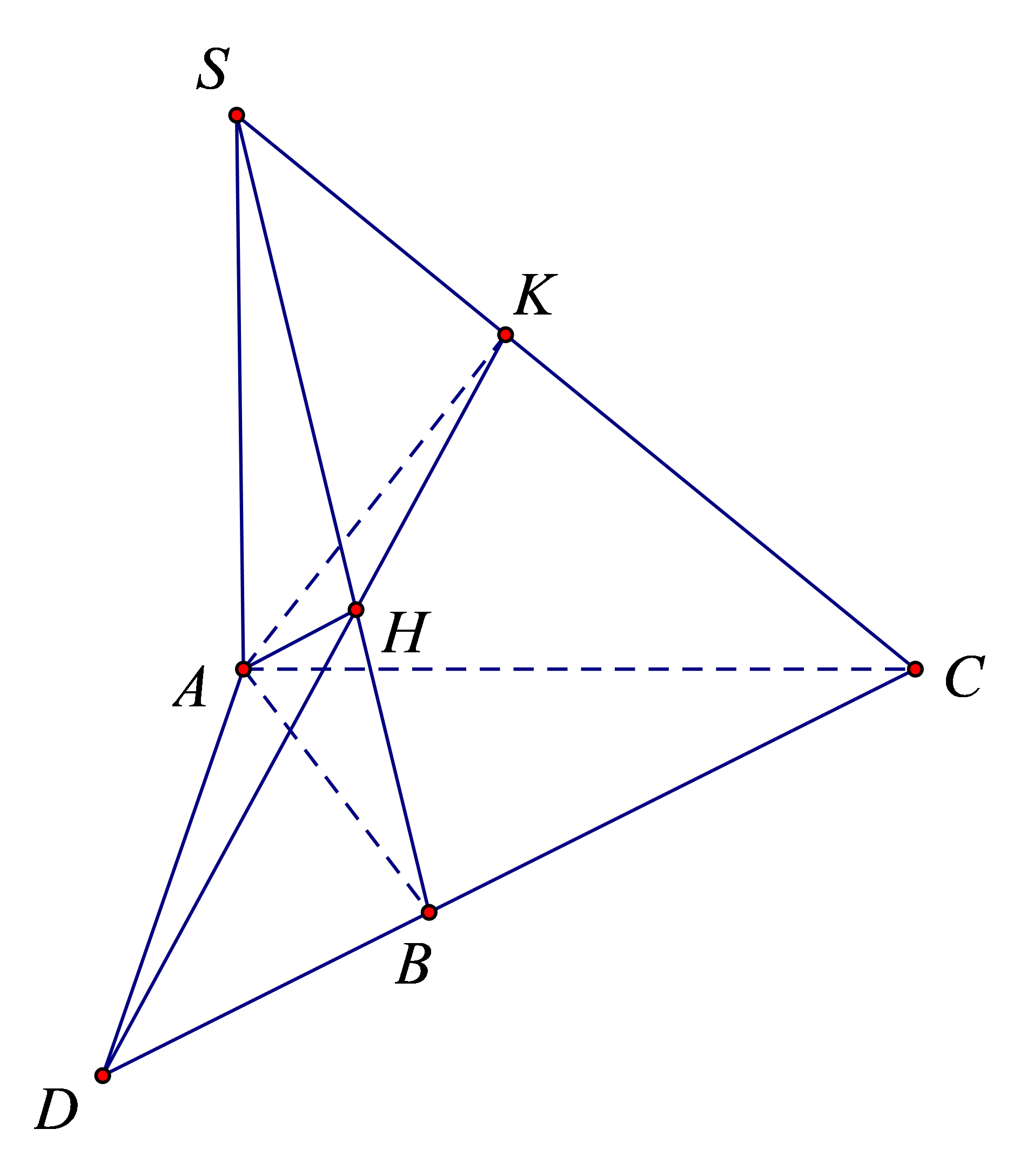
a) Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\) mà \(BC \bot AB\) \( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\( \Rightarrow \Delta SBC\) là tam giác vuông tại \(B\).
b) Vì \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\) mà \(AH \bot SB\) nên \(AH \bot \left( {SBC} \right)\).
c) Vì \(AH \bot \left( {SBC} \right)\) nên \(AH \bot SC\) mà \(AK \bot SC\)\( \Rightarrow SC \bot \left( {AHK} \right) \Rightarrow SC \bot HK\) hay \(\left( {SC,HK} \right) = 90^\circ \).
d) Vì \(HK \bot SC\) và \(AK \bot SC\) nên \(SC \bot \left( {ADK} \right) \Rightarrow AD \bot SC\) (1).
Mà \(SA \bot \left( {ADC} \right) \Rightarrow SA \bot AD\) (2).
Từ (1) và (2), suy ra \(AD \bot \left( {SAC} \right) \Rightarrow AD \bot AC\) hay \(\left( {AC,AD} \right) = 90^\circ \).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập