(3,0 điểm)
1) Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính:
a) Diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\)
b) Thể tích của hình chóp \(S.ABC,\) biết chiều cao \(SO\) của hình chóp là \(5,8{\rm{\;cm}}.\)
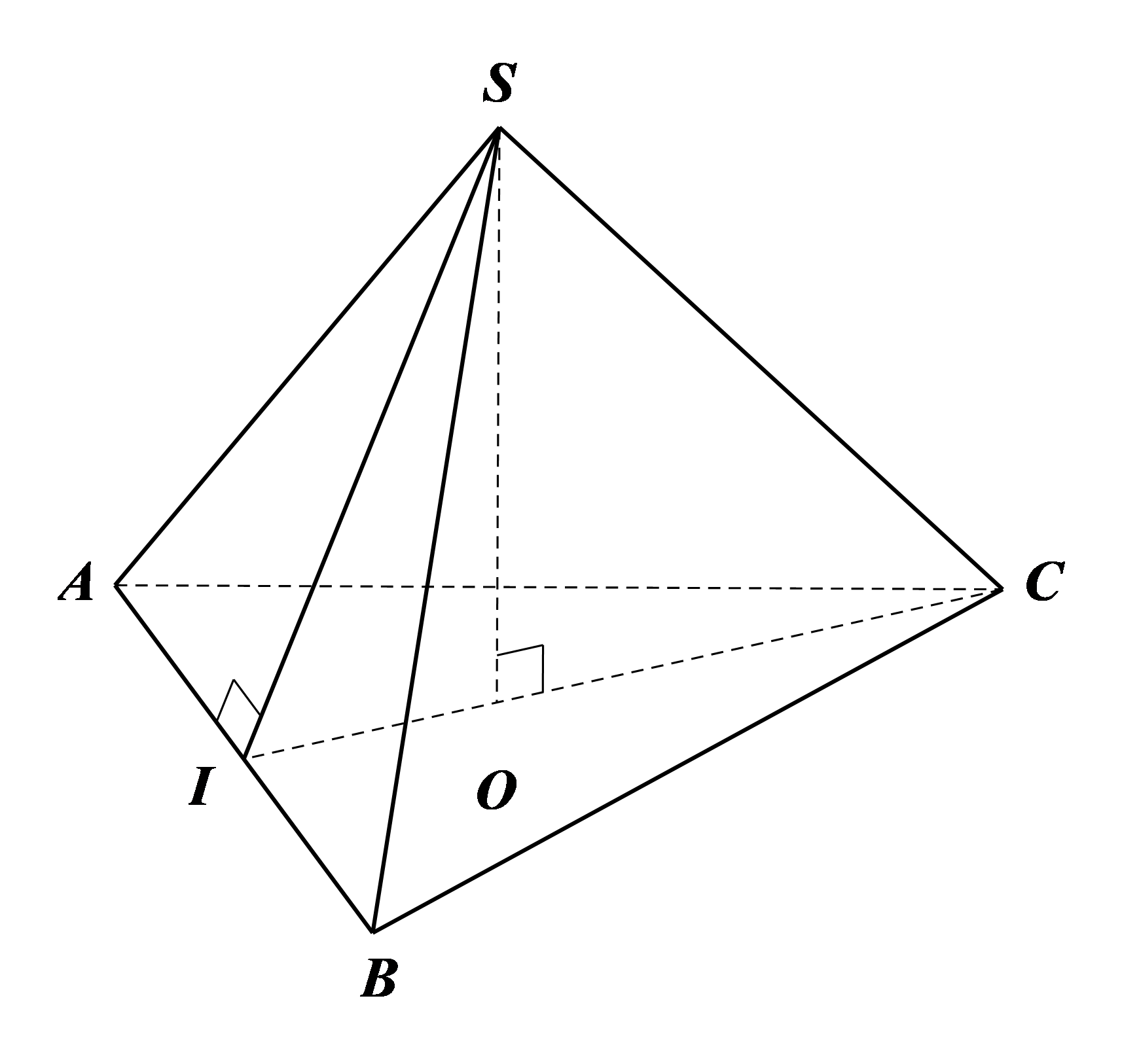
(Làm tròn các kết quả đến chữ số thập phân thứ hai).
2) Cho hình bình hành \(ABCD\) có \(BC = 2AB,\) \(\widehat {A\,\,} = 60^\circ .\) Gọi \(E\), \(F\) theo thứ tự là trung điểm của \(BC,\) \(AD.\) Trên tia \(AB\) lấy điểm \(I\) sao cho \(B\) là trung điểm của \(AI.\)
a) Tứ giác \(ABEF\) là hình gì? Vì sao?
b) Tính \(\widehat {AED}.\)
(3,0 điểm)
|
1) Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính: a) Diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\) b) Thể tích của hình chóp \(S.ABC,\) biết chiều cao \(SO\) của hình chóp là \(5,8{\rm{\;cm}}.\) |
|
(Làm tròn các kết quả đến chữ số thập phân thứ hai).
2) Cho hình bình hành \(ABCD\) có \(BC = 2AB,\) \(\widehat {A\,\,} = 60^\circ .\) Gọi \(E\), \(F\) theo thứ tự là trung điểm của \(BC,\) \(AD.\) Trên tia \(AB\) lấy điểm \(I\) sao cho \(B\) là trung điểm của \(AI.\)
a) Tứ giác \(ABEF\) là hình gì? Vì sao?
b) Tính \(\widehat {AED}.\)
Câu hỏi trong đề: Bộ 10 đề thi cuối kì Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
1)
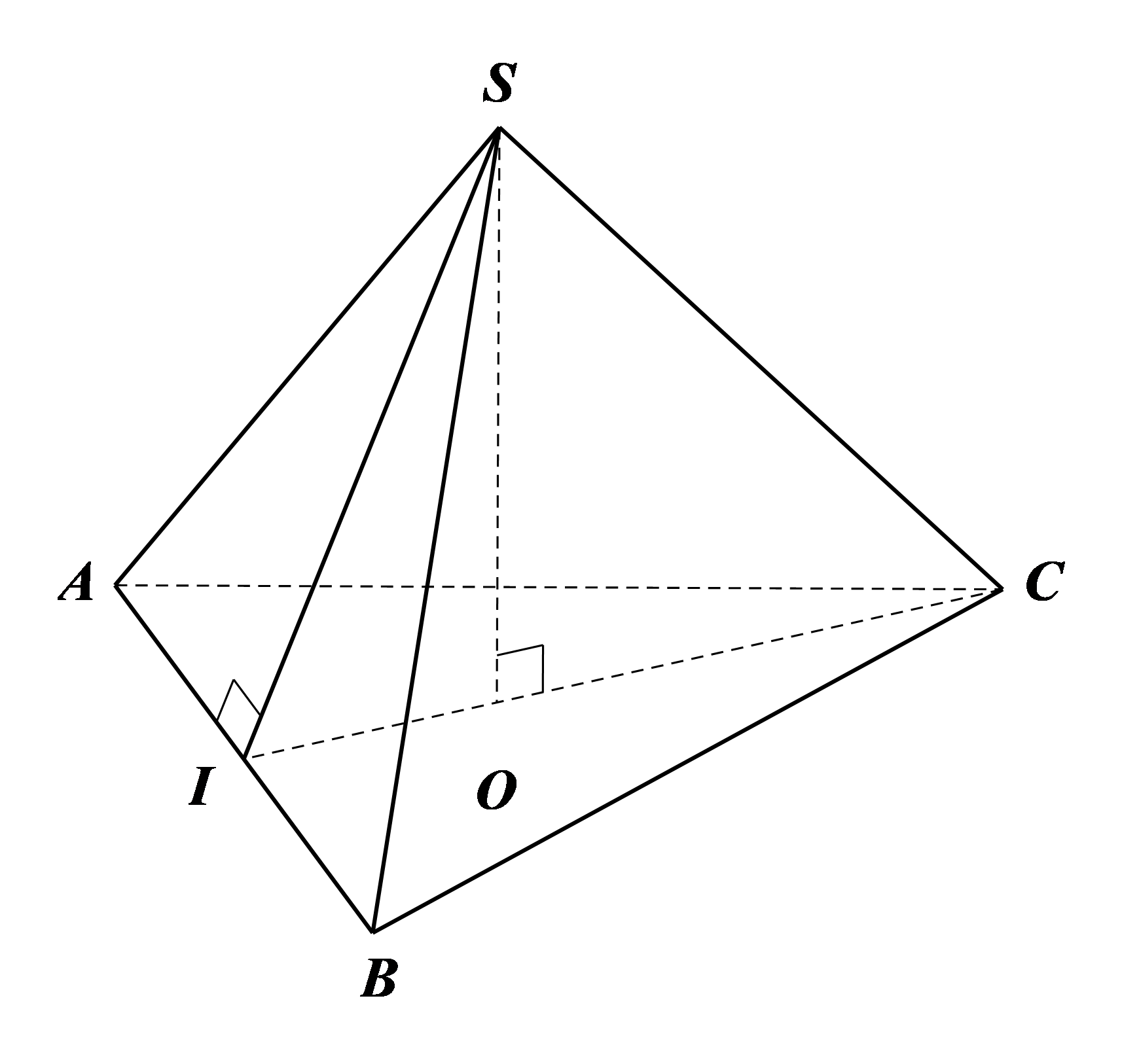
a) Diện tích xung quanh của hình chóp tam giác đều \(S.ABC\) là:
\({S_{xq}} = \frac{1}{2} \cdot \left( {AB + BC + CA} \right) \cdot SI = \frac{1}{2} \cdot \left( {5 + 5 + 5} \right) \cdot 6 = 45{\rm{\;}}\left( {{\rm{c}}{{\rm{m}}^2}} \right){\rm{.}}\)
Tam giác \(ABC\) là tam giác đều nên đường trung tuyến \(CI\) đồng thời là đường cao.
Xét \(\Delta ACI\) vuông tại \(I\) có \(A{C^2} = A{I^2} + C{I^2}\)
Suy ra \(C{I^2} = A{C^2} - A{I^2} = {5^2} - {\left( {\frac{1}{2} \cdot 5} \right)^2} = 25 - \frac{{25}}{4} = \frac{{75}}{4}\)
Do đó \(CI = \sqrt {\frac{{75}}{4}} \approx 4,33{\rm{\;cm}}.\)
Diện tích đáy của hình chóp tam giác đều \(S.ABC\) là:
Diện tích toàn phần của hình chóp tam giác đều \(S.ABC\) là:
b) Thể tích của hình chóp tam giác đều \(S.ABC\) là:
2)
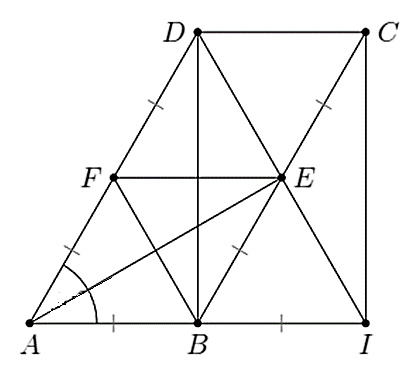
a) Do tứ giác \(ABCD\) là hình bình hành nên \(AD = BC,\,\,AD\,{\rm{//}}\,BC\).
Vì \(AD = BC,\) \(BE = \frac{1}{2}BC\) và \(AF = \frac{1}{2}AD\) (do \(F\) là trung điểm của \(AD)\) nên \(BE = AF.\)
Tứ giác \(ABEF\) có \(BE = AF\) và \(BE\,{\rm{//}}\,AF\) (vì \(AD\,{\rm{//}}\,BC)\)
Suy ra, tứ giác \(ABEF\) là hình bình hành.
Do \(E\) là trung điểm của \(BC\) nên \(BE = \frac{1}{2}BC\) hay \(BC = 2BE.\)
Vì \(BC = 2AB\) và \(BC = 2BE\) nên \(AB = BE\).
Hình bình hành \(ABEF\) có \(AB = BE\) nên \(ABEF\) là hình thoi.
b) Vì tứ giác \(ABCD\) là hình bình hành nên \(AB = CD,\,\,AB\,{\rm{//}}\,CD\).
Vì \(AB = CD\) và \(AB = BI\) (do \(B\) là trung điểm của \(AI)\) nên \(BI = CD\).
Tứ giác \(BICD\) có \(BI\,{\rm{//}}\,CD\) (vì \(AB\,{\rm{//}}\,CD)\) và \(BI = CD\) nên tứ giác \(BICD\) là hình bình hành.
Ta thấy \(BD\) vừa là đường trung tuyến vừa là đường phân giác của tam giác \(ADI\) nên tam giác \(ADI\) cân tại \(D\).
Suy ra \(BD\) cũng là đường cao của tam giác \(ADI\) nên \(BD \bot BI\) hay \(\widehat {DBI} = 90^\circ .\)
Hình bình hành \(BICD\) có \(\widehat {DBI} = 90^\circ \) nên tứ giác \(BICD\) là hình chữ nhật.
Khi đó, \(E\) là trung điểm của hai đường chéo \(BC\) và \(DI\).
Tam giác \(ADI\) cân tại \(D\) có \(\widehat {DAI} = 60^\circ \) nên tam giác \(ADI\) là tam giác đều.
\(\Delta ADI\) là tam giác đều có \(AE\) là đường trung tuyến nên đồng thời là đường cao.
Do đó, \(AE \bot DI\) hay \(\widehat {AED} = 90^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Theo đề bài: \({x^2} + \frac{8}{{{x^2}}} + \frac{{{y^2}}}{8} = 8\) suy ra \(2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = 16\)
Ta có: \[2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = \left( {{x^2} + \frac{{16}}{{{x^2}}} - 8} \right) + \left( {{x^2} + \frac{{{y^2}}}{4} + xy} \right) - xy + 8\]
\[ = {\left( {x - \frac{4}{x}} \right)^2} + {\left( {x + \frac{y}{2}} \right)^2} - xy + 8.\]
Mà \(2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = 16\) nên \[{\left( {x - \frac{4}{x}} \right)^2} + {\left( {x + \frac{y}{2}} \right)^2} - xy + 8 = 16\].
Do đó \[{\left( {x - \frac{4}{x}} \right)^2} + {\left( {x + \frac{y}{2}} \right)^2} = xy + 8.\]
Nhận xét: Với mọi \(x,y\) ta có \[{\left( {x - \frac{4}{x}} \right)^2} \ge 0,\,\,{\left( {x + \frac{y}{2}} \right)^2} \ge 0\]
Do đó \[xy + 8 \ge 0\] hay \[xy \ge - 8.\]
Khi đó \(A = xy + 2\,\,024 \ge - 8 + 2\,\,024 = 2\,\,016.\)
Dấu “=” xảy ra khi và chỉ khi \[\left\{ \begin{array}{l}{\left( {x - \frac{4}{x}} \right)^2} = 0\\{\left( {x + \frac{y}{2}} \right)^2} = 0\end{array} \right.\] hay \[\left\{ \begin{array}{l}x - \frac{4}{x} = 0\\x + \frac{y}{2} = 0\end{array} \right.\]
Tức là \[\left\{ \begin{array}{l}{x^2} - 4 = 0\\y = - 2x\end{array} \right.\] nên \[\left\{ \begin{array}{l}x = 2\\y = - 4\end{array} \right.\] hoặc \[\left\{ \begin{array}{l}x = - 2\\y = 4\end{array} \right..\]
Vậy giá trị nhỏ nhất của biểu thức \(A\) là \(2\,\,016\) khi \(\left( {x;y} \right) \in \left\{ {\left( {2; - 4} \right);\left( { - 2;4} \right)} \right\}.\)
Lời giải
Hướng dẫn giải
a) Mức giá khi lượng cung bằng lượng cầu là giá trị \[{x_0}\] thỏa mãn:
\[30{x_0} = 1{\rm{ }}800\]
\[{x_0} = 60\]
Vậy mức giá cân bằng là 60 nghìn đồng.
b) Đồ thị hàm số \[S\left( p \right)\] đi qua hai điểm \[\left( {0;--600} \right)\] và \[\left( {60;{\rm{ }}0} \right).\]
Đồ thị hàm số \[D\left( p \right)\] đi qua hai điểm \[\left( {0;{\rm{ }}1{\rm{ }}200} \right)\] và \[\left( {60;{\rm{ }}0} \right).\]
Đồ thị của hai hàm số được vẽ trong hình dưới:
![Giả sử rằng lượng cung \[S\] và lượ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/6-1765167270.png)
c) Từ đồ thị trên, ta thấy khi giá của mỗi chiếc áo lớn hơn 60 nghìn đồng thì lượng cung lớn hơn lượng cầu. Khi đó sẽ có một lượng áo phông bị tồn kho (do không bán được).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.