C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho \(F\left( x \right)\) và \(G\left( x \right)\) là hai nguyên hàm của hàm số \(f\left( x \right)\) và thỏa mãn \(F\left( 0 \right) = G\left( 0 \right) + 1\). Khi đó, nếu \(\int\limits_3^6 {F\left( x \right){\rm{d}}x} = 27\) thì \(\int\limits_3^6 {G\left( x \right){\rm{d}}x} \)bằng bao nhiêu?
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho \(F\left( x \right)\) và \(G\left( x \right)\) là hai nguyên hàm của hàm số \(f\left( x \right)\) và thỏa mãn \(F\left( 0 \right) = G\left( 0 \right) + 1\). Khi đó, nếu \(\int\limits_3^6 {F\left( x \right){\rm{d}}x} = 27\) thì \(\int\limits_3^6 {G\left( x \right){\rm{d}}x} \)bằng bao nhiêu?
Quảng cáo
Trả lời:
Trả lời: 24
Ta có \(F\left( x \right) = G\left( x \right) + C\) mà \(F\left( 0 \right) = G\left( 0 \right) + 1\) nên \(C = 1\).
Do đó \(F\left( x \right) = G\left( x \right) + 1\). Khi đó
\(27 = \int\limits_3^6 {F\left( x \right){\rm{d}}x} = \int\limits_3^6 {\left( {G\left( x \right) + 1} \right)dx} = \int\limits_3^6 {G\left( x \right)dx} + \left. x \right|_3^6 = \int\limits_3^6 {G\left( x \right)dx} + 3 \Rightarrow \int\limits_3^6 {G\left( x \right)dx} = 27 - 3 = 24\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) S, b) Đ, c) Đ, d) Đ
a) Mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến \(\overrightarrow n = \left( {2;1; - 2} \right)\).
Thay tọa độ điểm \(A\) vào phương trình mặt phẳng \(\left( P \right)\) ta thấy không thỏa mãn. Do đó \(A \notin \left( P \right)\).
b) Ta có \(d\left( {A,\left( P \right)} \right) = \frac{{\left| {2.\left( { - 1} \right) + 0 - 2.2} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = 2\).
c) Mặt phẳng \(\left( Q \right)\) song song với mặt phẳng \(\left( P \right)\) có dạng \(2x + y - 2z + d = 0\left( {d \ne 0} \right)\).
Vì \(\left( Q \right)\) đi qua \(A\left( { - 1;0;2} \right)\) nên \(2.\left( { - 1} \right) + 0 - 2.2 + d = 0 \Leftrightarrow d = 6\)(thỏa mãn).
Vậy \(\left( Q \right):2x + y - 2z + 6 = 0\).
d) Có \(\overrightarrow {OA} = \left( { - 1;0;2} \right),\overrightarrow {{n_P}} = \left( {2;1; - 2} \right)\), \(\left[ {\overrightarrow {OA} ,\overrightarrow {{n_P}} } \right] = \left( { - 2;2; - 1} \right) = - \left( {2; - 2;1} \right)\).
Vậy mặt phẳng đi qua gốc tọa độ O, điểm \(A\) và vuông góc \(\left( P \right)\) có một vectơ pháp tuyến là \(\left( {2; - 2;1} \right).\)
Lời giải
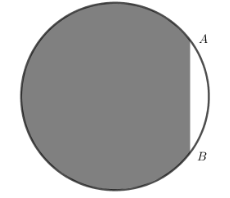
Diện tích miếng tôn hình tròn là \({S_1} = \pi {R^2} = 25\pi \left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ
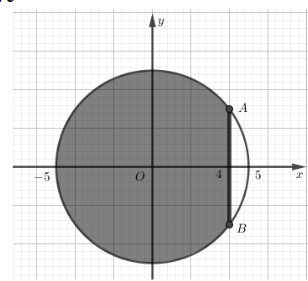
Phương trình của đường tròn tâm \(O\), bán kính bằng 5 là \({x^2} + {y^2} = 25\).
Phương trình nửa phía trên trục hoành của đường tròn là \(y = \sqrt {25 - {x^2}} \).
Có \(AB = 6 \Rightarrow {y_A} = 3 \Rightarrow {x_A} = 4\).
Vậy diện tích phần tấm trống là \({S_2} = 2\int\limits_4^5 {\sqrt {25 - {x^2}} } dx\).
Diện tích phần tấm tôn trang trí là \(S = {S_1} - {S_2} = 25\pi - 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} \).
Vậy số tiền cần trả là \(100.\left( {25\pi - 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} } \right) \approx 7445\) nghìn đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.