Ông An muốn thuê một chiếc xe ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

	Phí cố định (nghìn đồng/ngày)	Phí tính theo quãng đường di chuyển (nghìn đồng/kilômét)
Từ thứ Hai đến thứ Sáu	900	8
Thứ Bảy và Chủ nhật	1500	10

Gọi \(x,y\) lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Biết rằng tổng số tiền ông An phải trả không vượt quá 14 triệu đồng. Bất phương trình nào dưới đây biểu thị mối liên hệ giữa \(x\) và \(y\)?

Miền nghiệm của hệ bất phương trình là miền tam giác \(ABC\), kể cả các cạnh (phần tô màu) như hình vẽ với \(A\left( { - 5; - 1} \right),B\left( { - 1; - 2} \right),C\left( {5;4} \right)\).

Biểu thức \(T = 3x - 2y - 4\) đạt giá trị nhỏ nhất tại một trong ba điểm \(A\left( { - 5; - 1} \right),B\left( { - 1; - 2} \right),C\left( {5;4} \right)\).

Ta có \(T\left( { - 5, - 1} \right) = 3 \cdot \left( { - 5} \right) - 2 \cdot \left( { - 1} \right) - 4 = - 17\); \(T\left( { - 1, - 2} \right) = 3 \cdot \left( { - 1} \right) - 2 \cdot \left( { - 2} \right) - 4 = - 3\);

\(T\left( {5,4} \right) = 3 \cdot 5 - 2 \cdot 4 - 4 = 3\).

Vậy giá trị nhỏ nhất của T là \( - 17\) khi \(x = - 5;y = - 1\).

Suy ra \(x_0^2 + y_0^2 = 26\).

a) Hệ bất phương trình trên là hệ bất phương trình bậc nhất hai ẩn.

b) Thay cặp số \(\left( {x;y} \right) = \left( {1;3} \right)\) vào hệ bất phương trình ta được \(\left\{ \begin{array}{l} - 2 \cdot 1 + 3 \le 2\\ - 1 + 2 \cdot 3 \ge 4\\1 + 3 \le 5\end{array} \right.\) (đúng).

Vậy cặp số \(\left( {x;y} \right) = \left( {1;3} \right)\) là nghiệm của hệ bất phương trình trên.

c) Miền nghiệm D của hệ là miền tam giác \(ABC\), kể cả các cạnh (phần tô màu) với \(A\left( {0;2} \right),B\left( {2;3} \right),C\left( {1;4} \right)\)

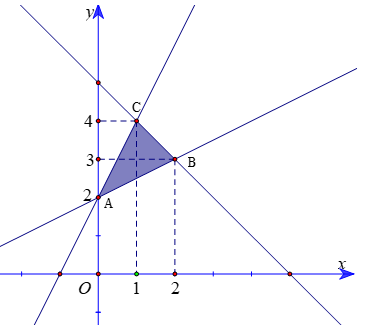
d) Biểu thức \(F\left( {x,y} \right) = - x + y\) đạt giá trị nhỏ nhất tại một trong 3 điểm \(A\left( {0;2} \right),B\left( {2;3} \right),C\left( {1;4} \right)\).

Khi đó \(F\left( {0,2} \right) = 0 + 2 = 2\); \(F\left( {2,3} \right) = - 2 + 3 = 1\); \(F\left( {1,4} \right) = - 1 + 4 = 3\).

Vậy giá trị nhỏ nhất của biểu thức \(F\left( {x,y} \right) = - x + y\) trên miền D xác định bởi hệ trên bằng 1.

Đáp án: a) Đúng;     b) Đúng;    c) Sai;    d) Đúng.