Trong không gian \(Oxyz\), cho hai điểm \(A\left( {4; - 2;4} \right),B\left( { - 2;6;4} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = 5\\y = - 1\\z = t\end{array} \right.\). Gọi \(M\) là điểm di động thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(\widehat {AMB} = 90^\circ \) và \(N\) là điểm di động thuộc \(d.\) Tìm giá trị nhỏ nhất của \(MN.\)
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {4; - 2;4} \right),B\left( { - 2;6;4} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = 5\\y = - 1\\z = t\end{array} \right.\). Gọi \(M\) là điểm di động thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(\widehat {AMB} = 90^\circ \) và \(N\) là điểm di động thuộc \(d.\) Tìm giá trị nhỏ nhất của \(MN.\)
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 12 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
Trả lời: 2
\(\left( {Oxy} \right)\) có 1 vectơ pháp tuyến \(\overrightarrow k = \left( {0;0;1} \right)\).
\(d\) có 1 vectơ chỉ phương \(\overrightarrow u = \left( {0;0;1} \right)\). Nên \(d \bot \left( {Oxy} \right)\).
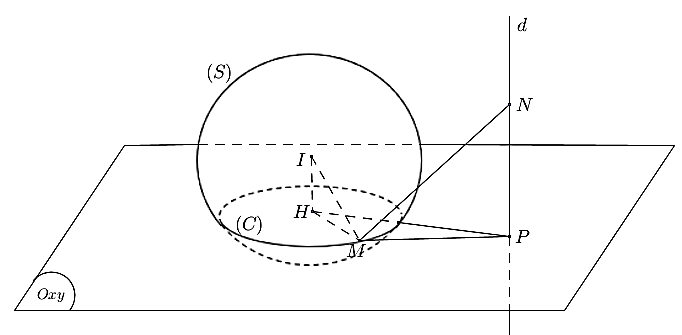
Gọi \(P = d \cap \left( {Oxy} \right) \Rightarrow P\left( {5; - 1;0} \right)\)
Gọi \(I\)là trung điểm \(AB\) \( \Rightarrow I\left( {1;2;4} \right)\).
\(\widehat {AMB} = 90^\circ \)\( \Rightarrow M\) thuộc mặt cầu \(\left( S \right)\) đường kính \(AB\), bán kính \(R = \frac{{AB}}{2} = \frac{{\sqrt {{{\left( { - 6} \right)}^2} + {8^2} + {0^2}} }}{2} = 5.\)
Mà \(M \in \left( {Oxy} \right)\) nên \(M\) thuộc đường tròn \(\left( C \right)\) là giao của mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( {Oxy} \right)\).
Gọi \(H\) là hình chiếu của \(I\) lên mặt phẳng \(\left( {Oxy} \right)\) \[ \Rightarrow H\left( {1;2;0} \right)\].
Suy ra \(M\) thuộc đường tròn \(\left( C \right)\) tâm \[H\left( {1;2;0} \right)\], bán kính \(r = \sqrt {{R^2} - I{H^2}} = \sqrt {25 - 16} = 3\).
Ta có: \(MN \ge MP \ge HP - r = \sqrt {16 + 9} - 3 = 2\).
Vậy \(M{N_{\min }} = 2\).
Dấu “=” xảy ra khi \(N \equiv P\) và \(H,M,P\) thẳng hàng (\(M\) nằm giữa \(H,P\)).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đ, b) S, c) S, d) S
a) \(\int\limits_0^1 {f\left( x \right)dx} = \left. {F\left( x \right)} \right|_0^1 = F\left( 1 \right) - F\left( 0 \right) = - \frac{7}{2}\).
b) \(\int\limits_0^2 {f\left( x \right)dx = \left. {F\left( x \right)} \right|_0^2 = F\left( 2 \right) - F\left( 0 \right) = - 2} \) mà \(F\left( 0 \right) = 3\) nên \(F\left( 2 \right) = 1\).
c) \(\int {f\left( x \right)} dx = \int {\left( {a{x^2} + bx + c} \right)dx} = \frac{a}{3}{x^3} + \frac{b}{2}{x^2} + cx + C\).
d) Vì \(\int\limits_0^1 {f\left( x \right)dx} = - \frac{7}{2}\) nên \(\frac{a}{3} + \frac{b}{2} + c = - \frac{7}{2}\) (1) và \(\int\limits_0^2 {f\left( x \right)dx = - 2} \) nên \(\frac{{8a}}{3} + 2b + 2c = - 2\) (2).
Từ (1) và (2), ta có
\( \Rightarrow \left\{ \begin{array}{l}2a + 3\left( {5 - 2a} \right) + 6c = - 21\\b = 5 - 2a\end{array} \right.\)\[ \Rightarrow \left\{ \begin{array}{l} - 2a + 3c = - 18\\b = 5 - 2a\end{array} \right.\]\[ \Rightarrow \left\{ \begin{array}{l}c = \frac{{ - 18 + 2a}}{3}\\b = 5 - 2a\end{array} \right.\].
Do đó \(a + b + 3c = a + 5 - 2a - 18 + 2a = a - 13\).
Câu 2
Lời giải
a) S, b) S, c) S, d) Đ
Gọi A là biến cố: “Sản phẩm bị thất lạc là sản phẩm loại II”
B là biến cố: “Sản phẩm bị thất lạc là sản phẩm loại I”
C là biến cố “Lấy được sản phẩm loại I từ 19 sản phẩm còn lại”.
a) Xác suất sản phẩm bị thất lạc là sản phẩm loại II là \(P\left( A \right) = \frac{{17}}{{20}}\).
b) Ta có \(P\left( {C|A} \right) = \frac{{P\left( {C \cap A} \right)}}{{P\left( A \right)}} = \frac{3}{{19}}\).
c) Ta có \(P\left( {C|B} \right) = \frac{2}{{19}}\).
d) Ta có \(P\left( C \right) = P\left( A \right).P\left( {C|A} \right) + P\left( B \right).P\left( {C|B} \right) = \frac{{17}}{{20}}.\frac{3}{{19}} + \frac{3}{{20}}.\frac{2}{{19}} = \frac{3}{{20}} = 15\% \).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.