Trong văn bản Thông điệp nhân ngày thế giới phòng chống AIDS, 1 – 12 – 2003, để tăng độ tin cậy và tính thuyết phục khi tổng kết tình hình cuộc đấu tranh chống đại dịch HIV/AIDS, Cô-phi An-nan đã
Trong văn bản Thông điệp nhân ngày thế giới phòng chống AIDS, 1 – 12 – 2003, để tăng độ tin cậy và tính thuyết phục khi tổng kết tình hình cuộc đấu tranh chống đại dịch HIV/AIDS, Cô-phi An-nan đã
Quảng cáo
Trả lời:
Đáp án
đưa ra những nhận định, đánh giá tổng hợp, bao quát nhưng vẫn có trọng điểm với những thông tin, số liệu cụ thể, chi tiết, có tính chọn lọc và rất kịp thời.
Giải thích
Trong văn bản Thông điệp nhân ngày thế giới phòng chống AIDS, 1 – 12 – 2003, khi tổng kết tình hình đấu tranh phòng chống đại dịch AIDS, tác giả đưa ra những nhận định, đánh giá tổng hợp kết hợp như: ngân sách dành cho phòng chống HIV tăng, nhiều nhóm từ thiện và cộng đồng đã tham gia vào nỗ lực chung phòng chống AIDS, tỉ lệ tử vong do AIDS cao, tốc độ lây lan ở phụ nữ có chiều hướng tăng nhanh... với việc đưa ra những số liệu cụ thể một cách có chọn lọc (cứ một phút đồng hồ trôi đi lại có thêm 10 người nhiễm HIV, phụ nữ chiếm một nửa số người nhiễm HIV trên thế giới... ) để làm cho chủ đề văn bản được tập trung, dung lượng văn bản ngắn gọn và hàm súc hơn đồng thời khiến cho người đọc, người nghe có được cái nhìn bao quát, chính xác về tình hình thực tế.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
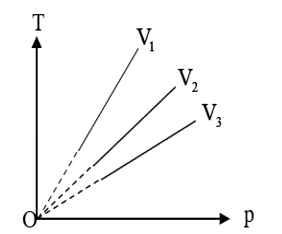
C. V3 < V2 < V1.
Lời giải
Đáp án
V3 < V2 < V1.
Giải thích
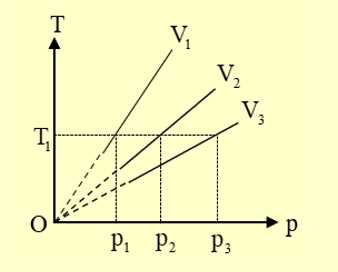
Ứng với nhiệt độ T1 ta có: p1 < p2 < p3
Do nhiệt độ không đổi, áp dụng định luật Boyle, ta có:
\({p_1}{V_1} = {p_2}{V_2} = {p_3}{V_3} \to {V_1} > {V_2} > {V_3}\).
Lời giải
Đáp án
80.
Giải thích
Ta có: \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left[ {3.{{\left( {{3^x}} \right)}^2} + {{2.3}^x} - 1} \right]\left( {{3^x} - y} \right) \le 0\)
\( \Leftrightarrow \left( {{3^x} + 1} \right)\left( {{{3.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left( {{3^{x + 1}} - 1} \right)\left( {{3^x} - y} \right) \le 0\) (do \({3^x} + 1 > 0,\forall x\)).
TH1. \({3^{x + 1}} - 1 \le 0 \Rightarrow x + 1 \le 0 \Leftrightarrow x \le - 1\) ta có \({3^x} - y \ge 0 \Rightarrow y \le {3^x} \le {3^{ - 1}} = \frac{1}{3}\) (vô lý vì \(y\) là số nguyên dương).
TH2. \({3^{x + 1}} - 1 \ge 0 \Rightarrow x + 1 \ge 0 \Leftrightarrow x \ge - 1\) ta có \({3^x} - y \le 0 \Rightarrow y \ge {3^x} \ge {3^{ - 1}} = \frac{1}{3}\) (luôn đúng vì \(y\) là số nguyên dương).
Để ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn bất phương trình nên nghiệm \(x\) chỉ nằm trong khoảng \(\left\{ { - 1;0;1;2;3} \right\} \Rightarrow y < {3^4} = 81\).
Vậy có 80 số nguyên dương \(y\) thỏa mãn yêu cầu đề bài.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.