Có V lít khí A gồm H2 và hai alkene là đồng đẳng liên tiếp, trong đó H2 chiếm 60% về thể tích. Dẫn hỗn hợp A qua bột Ni nung nóng được hỗn hợp khí B. Đốt cháy hoàn toàn khí B được 19,8 gRam CO2 và 13,5 gam H2O. Công thức của hai alkene là.
Quảng cáo
Trả lời:
Đáp án
C2H4 và C3H6.
Giải thích
Đặt CTTB của hai alkene là \({C_{\bar n}}{H_{2\bar n}}\)
Ở cùng điều kiện nhiệt độ và áp suất thì thể tích tỷ lệ với số mol khí.
Hỗn hợp khí A có\(\frac{{{n_{{C_{\bar n}}{H_{2\bar n}}}}}}{{{n_{{H_2}}}}} = \frac{{0,4}}{{0,6}} = \frac{2}{3}\).
Áp dụng định luật bảo toàn khối lượng và định luật bảo toàn nguyên tử
Đốt cháy hỗn hợp khí B cũng chính là đốt cháy hỗn hợp khí A. Ta có.
(1)
2H2 + O2 → 2H2O (2)
Theo phương trình (1) ta có.
\({n_{{\rm{C}}{{\rm{O}}_2}}} = {n_{{{\rm{H}}_2}{\rm{O}}}} = 0,45\) mol.\( \Rightarrow {n_{{C_{\bar n}}{H_{2\bar n}}}} = \frac{{0,45}}{{\bar n}}\)\({n_{{H_2}O}} = \frac{{13,5}}{{18}} = 0,75\)
mol.
Tổng mol
\( \Rightarrow {n_{{H_2}O}}_{\,(pt\,2)} = 0,75 - 0,45 = 0,3\) mol
\( \Rightarrow {n_{{H_2}}} = 0,3\) mol.
Ta có \(\frac{{{n_{{C_{\bar n}}{H_{2\bar n}}}}}}{{{n_{{H_2}}}}} = \frac{{0,45}}{{0,3.\bar n}} = \frac{2}{3}\)
\( \Rightarrow \bar n = 2,25\)
\( \Rightarrow \) Hai alkene đồng đẳng liên tiếp là C2H4 và C3H6.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
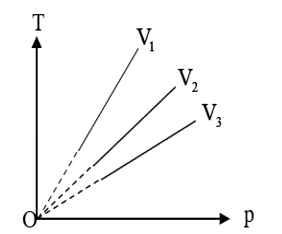
C. V3 < V2 < V1.
Lời giải
Đáp án
V3 < V2 < V1.
Giải thích
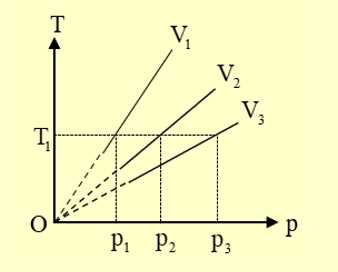
Ứng với nhiệt độ T1 ta có: p1 < p2 < p3
Do nhiệt độ không đổi, áp dụng định luật Boyle, ta có:
\({p_1}{V_1} = {p_2}{V_2} = {p_3}{V_3} \to {V_1} > {V_2} > {V_3}\).
Lời giải
Đáp án
80.
Giải thích
Ta có: \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left[ {3.{{\left( {{3^x}} \right)}^2} + {{2.3}^x} - 1} \right]\left( {{3^x} - y} \right) \le 0\)
\( \Leftrightarrow \left( {{3^x} + 1} \right)\left( {{{3.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left( {{3^{x + 1}} - 1} \right)\left( {{3^x} - y} \right) \le 0\) (do \({3^x} + 1 > 0,\forall x\)).
TH1. \({3^{x + 1}} - 1 \le 0 \Rightarrow x + 1 \le 0 \Leftrightarrow x \le - 1\) ta có \({3^x} - y \ge 0 \Rightarrow y \le {3^x} \le {3^{ - 1}} = \frac{1}{3}\) (vô lý vì \(y\) là số nguyên dương).
TH2. \({3^{x + 1}} - 1 \ge 0 \Rightarrow x + 1 \ge 0 \Leftrightarrow x \ge - 1\) ta có \({3^x} - y \le 0 \Rightarrow y \ge {3^x} \ge {3^{ - 1}} = \frac{1}{3}\) (luôn đúng vì \(y\) là số nguyên dương).
Để ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn bất phương trình nên nghiệm \(x\) chỉ nằm trong khoảng \(\left\{ { - 1;0;1;2;3} \right\} \Rightarrow y < {3^4} = 81\).
Vậy có 80 số nguyên dương \(y\) thỏa mãn yêu cầu đề bài.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.