Cho đường tròn \(\left( {O\,;\,R} \right)\)và điểm A sao cho \(OA\, > \,2R\). Từ A vẽ hai tiếp tuyến \(AB\,,\,\,\,AC\)của (O) (B, C là hai tiếp điểm). Vẽ dây cung CD của (O) song song với AB. Đường thẳng AD cắt (O) tại E khác A và cắt BC tại G. Qua G vẽ đường thẳng vuông góc với OG lần lượt cắt hai đường thẳng AB, AC tại M và N.
a) Chứng minh tam giác \(OMN\) cân
b) Gọi I là trung điểm của DE, OA cắt BC tại K. Chứng minh: \(I{E^2} = IA \cdot IG\)
c) Tia BE cắt AC ở H . Chứng minh CE đi qua trung điểm của HG.
Cho đường tròn \(\left( {O\,;\,R} \right)\)và điểm A sao cho \(OA\, > \,2R\). Từ A vẽ hai tiếp tuyến \(AB\,,\,\,\,AC\)của (O) (B, C là hai tiếp điểm). Vẽ dây cung CD của (O) song song với AB. Đường thẳng AD cắt (O) tại E khác A và cắt BC tại G. Qua G vẽ đường thẳng vuông góc với OG lần lượt cắt hai đường thẳng AB, AC tại M và N.
a) Chứng minh tam giác \(OMN\) cân
b) Gọi I là trung điểm của DE, OA cắt BC tại K. Chứng minh: \(I{E^2} = IA \cdot IG\)
c) Tia BE cắt AC ở H . Chứng minh CE đi qua trung điểm của HG.
Quảng cáo
Trả lời:
Giải bởi Vietjack
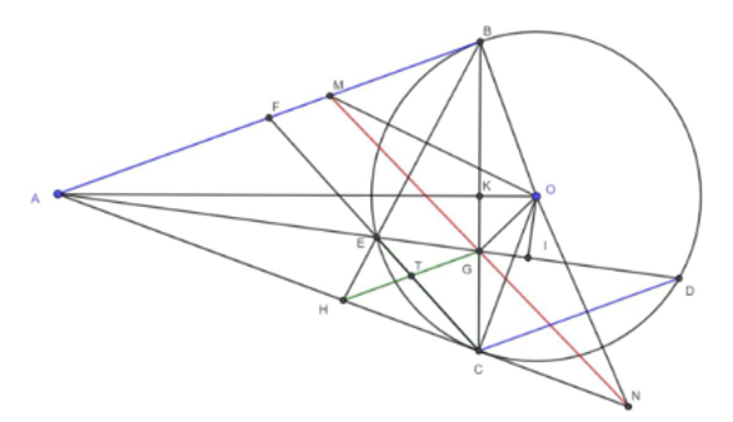
a) Tứ giác OGMB nội tiếp đường tròn đường kính MO \( \Rightarrow \widehat {OMG} = \widehat {OBG}.\)
Tứ giác OGCN nội tiếp đường tròn đường kính NO \( \Rightarrow \widehat {ONG} = \widehat {OCG}\)
Tuy nhiên tam giác OBC cân tại O \( \Rightarrow \widehat {OBC} = \widehat {OCB} \Rightarrow \widehat {OMG} = \widehat {ONG} \Rightarrow \Delta OMN\)cân tại O.
b) ta có: đồng dạng \( \Rightarrow AG.AI = AK.AO.\)
Mặt khác, dễ thấy: \(AK\,.\,AO = A{B^2}\) và \(A{B^2} = AE \cdot AD \Rightarrow AG \cdot AI = AE \cdot AD\)
Khi đó: \(AG \cdot AI = (AI - IE)(AI + IE) = A{I^2} - I{E^2} \Rightarrow I{E^2} = A{I^2} - AG \cdot AI = IG \cdot IA\)
c) Gọi T là giao điểm của HG và CE . Ta có: \(\widehat {BED} = \widehat {BCD} = \widehat {CBA} = \widehat {ACB} \Rightarrow HEGC\) là tứ giác nội tiếp.
\( \Rightarrow \widehat {HGC} = \widehat {HEC} = \widehat {CDB} = \widehat {CBA}.\)Đến đây ta chứng minh hai đường thẳng HG, AB song song với nhau .
Kéo dài CE cắt AB tại F.
Dễ thấy: \(\angle FAE = \angle EDC = \angle ECA \Rightarrow \Delta FAE,\Delta FCA\) đồng dạng \( \Rightarrow F{A^2} = FE\,.\,FC\), mà \(F{B^2} = FE\,.\,FC \Rightarrow F\)là trung điểm của AB. Đến đây sử dụng định lý Ta-lét , thì : \(\frac{{TG}}{{FB}} = \frac{{CT}}{{CF}} = \frac{{TH}}{{FA}} \Rightarrow TG = TH\) hay T là trung điểm của GH.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi D, E, F lần lượt là giao điểm của OA, OB, OC với các đường thẳng BC, CA, AB
Dễ thấy hai tam giác OCD, OMC đồng dạng \( \Rightarrow OD.OM = O{C^2} = 1 \Rightarrow OM = \frac{1}{{OD}}\)
Tương tự: \(ON = \frac{1}{{OE}};OP = \frac{1}{{OF}}\)
Đặt: \(x = {S_{{\rm{OBC }}}};y = {S_{OCA:}};z = {S_{OAB}} \Rightarrow \frac{1}{{OD}} = \frac{{OA}}{{OD}} = \frac{{y + z}}{x}\)
Tương tự: \(\frac{1}{{OE}} = \frac{{x + z}}{y};\frac{1}{{OF}} = \frac{{y + z}}{x}\)
Khi đó: \(\frac{1}{{OD}} + \frac{1}{{OE}} + \frac{1}{{OF}} = \left( {\frac{x}{y} + \frac{y}{x}} \right) + \left( {\frac{x}{z} + \frac{z}{x}} \right) + \left( {\frac{y}{z} + \frac{z}{y}} \right) \ge 6.\)
Do đó: \(S = \frac{1}{{O{D^2}}} + \frac{1}{{O{E^2}}} + \frac{1}{{O{F^2}}} \ge \frac{1}{3}{\left( {\frac{1}{{OD}} + \frac{1}{{OE}} + \frac{1}{{OF}}} \right)^2} \ge 12.\)
Vậy GTNN của biểu thức S là 12 đạt được khi tam giác ABC đều.
Lời giải
a) \(P = \left( {\frac{{\sqrt x (\sqrt x - 3)}}{{(\sqrt x + 1)(\sqrt x - 3)}} - \frac{{2x}}{{x - 1}}} \right):\frac{{1 - \sqrt x }}{{{{(\sqrt x - 1)}^2}}} = \frac{{\sqrt x (\sqrt x - 1) - 2x}}{{(\sqrt x - 1)(\sqrt x + 1)}}:\frac{{ - 1}}{{\sqrt x - 1}}\)
\( \Rightarrow P = \frac{{ - \sqrt x (\sqrt x + 1)}}{{(\sqrt x - 1)(\sqrt x + 1)}} \cdot ( - (\sqrt x - 1)) = \sqrt x \)
b) Điều kiện: \(x \ge - 2\). Phương trình \( \Leftrightarrow \left( {{x^2} - 2x + 4} \right) + (x + 2) - 2\sqrt {(x + 2)\left( {{x^2} - 2x + 4} \right)} = 0\)
\( \Leftrightarrow {\left( {\sqrt {{x^2} - 2x + 4} - \sqrt {x + 2} } \right)^2} = 0 \Leftrightarrow \sqrt {{x^2} - 2x + 4} = \sqrt {x + 2} \)
\( \Leftrightarrow {x^2} - 3x + 2 - 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 2}\end{array}} \right.\) (thỏa mãn ĐK)
Vậy tập nghiệm của phương trình đã cho là: \[{\rm{S = \{ 1 ; 2\} }}\]
c) Điều kiện: \({x^2} - y - 1 \ge 0\). Xét hệ pt: \(\left\{ {\begin{array}{*{20}{l}}{{y^2} - 2{x^2} - xy - y + 2x = 0\,\,\,(1)}\\{\sqrt {{x^2} - y - 1} + x + y = 1\,\,\,\,\,\,\,\,\,\,\,\,(2)}\end{array}} \right.\)
ta có: \((1) \Leftrightarrow (y - 2x)(y + x - 1) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 2x}\\{y = 1 - x}\end{array}} \right.\)
* Trường hợp 1: với \(y = 2x\) thay vào (2), thu được:
\(\sqrt {{x^2} - 2x - 1} = 1 - 3x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le \frac{1}{3}}\\{{x^2} - 2x - 1 = 1 - 6x + 9{x^2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le \frac{1}{3}}\\{8{x^2} - 4x + 2 = 0}\end{array}} \right.} \right.\) (vô nghiệm)
* Trường hợp 2: với \(y = 1 - x\) thay vào (2), thu được: \(\sqrt {{x^2} + x - 2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 2}\end{array}} \right.\)
Vậy tập nghiệm của hệ pt đã cho là: \[{\rm{S}}\,{\rm{ = }}\left\{ {{\rm{(1 ; 0) ;( - 2 ; 3)}}} \right\}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập