Cho đường tròn (O) bán kính 1. Ba điểm phân biệt A, B, C thay đổi nằm trên đường tròn (O) sao cho điểm O nằm bên trong tam giác ABC . Các đường thẳng OA, OB, OC lần lượt cắt đường tròn ngoại tiếp tam giác \[{\rm{OBC, OCA, OAB}}\] tại M, N, P khác O. Tìm giá trị nhỏ nhất của biểu thức: \(S = O{M^2} + O{N^2} + O{P^2}\)
Cho đường tròn (O) bán kính 1. Ba điểm phân biệt A, B, C thay đổi nằm trên đường tròn (O) sao cho điểm O nằm bên trong tam giác ABC . Các đường thẳng OA, OB, OC lần lượt cắt đường tròn ngoại tiếp tam giác \[{\rm{OBC, OCA, OAB}}\] tại M, N, P khác O. Tìm giá trị nhỏ nhất của biểu thức: \(S = O{M^2} + O{N^2} + O{P^2}\)
Quảng cáo
Trả lời:
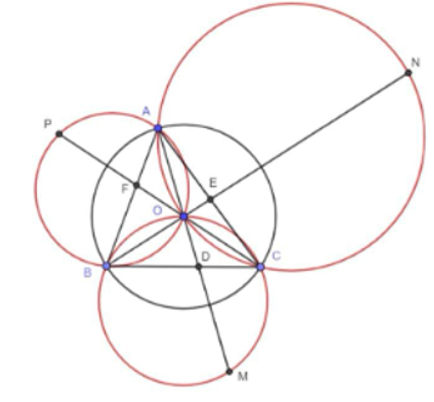
Gọi D, E, F lần lượt là giao điểm của OA, OB, OC với các đường thẳng BC, CA, AB
Dễ thấy hai tam giác OCD, OMC đồng dạng \( \Rightarrow OD.OM = O{C^2} = 1 \Rightarrow OM = \frac{1}{{OD}}\)
Tương tự: \(ON = \frac{1}{{OE}};OP = \frac{1}{{OF}}\)
Đặt: \(x = {S_{{\rm{OBC }}}};y = {S_{OCA:}};z = {S_{OAB}} \Rightarrow \frac{1}{{OD}} = \frac{{OA}}{{OD}} = \frac{{y + z}}{x}\)
Tương tự: \(\frac{1}{{OE}} = \frac{{x + z}}{y};\frac{1}{{OF}} = \frac{{y + z}}{x}\)
Khi đó: \(\frac{1}{{OD}} + \frac{1}{{OE}} + \frac{1}{{OF}} = \left( {\frac{x}{y} + \frac{y}{x}} \right) + \left( {\frac{x}{z} + \frac{z}{x}} \right) + \left( {\frac{y}{z} + \frac{z}{y}} \right) \ge 6.\)
Do đó: \(S = \frac{1}{{O{D^2}}} + \frac{1}{{O{E^2}}} + \frac{1}{{O{F^2}}} \ge \frac{1}{3}{\left( {\frac{1}{{OD}} + \frac{1}{{OE}} + \frac{1}{{OF}}} \right)^2} \ge 12.\)
Vậy GTNN của biểu thức S là 12 đạt được khi tam giác ABC đều.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: \((x + y)\left( {{x^2} - 2y + 2} \right) = - 1\). Do đó có hai khả năng xảy ra:
\({\rm{ TH1: }}\left\{ {\begin{array}{*{20}{l}}{x + y = 1}\\{{x^2} - 2y + 2 = - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 1 - x}\\{{x^2} + 2x + 1 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 1}\\{y = 2}\end{array}} \right.} \right.} \right.{\rm{. }}\)
\({\rm{ TH2: }}\left\{ {\begin{array}{*{20}{l}}{x + y = - 1}\\{{x^2} - 2y + 2 = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = - 1 - x}\\{{x^2} + 2x + 3 = 0}\end{array}} \right.} \right.\) (vô nghiệm)
Vậy có duy nhất cặp số nguyên \(\left( {x\,,\,y} \right)\)thỏa mãn yêu cầu là: \[{\rm{( - 1 ; 2) }}{\rm{.}}\]
b) Ta chia hình vuông ABCD thành 36 hình vuông có độ dài cạnh bằng 2. Khi đó có ít nhất một hình vuông không chứa điểm nào trong 31 điểm đã cho . Hình tròn nội tiếp hình vuông đã cho là hình tròn thỏa mãn yêu cầu bài toán.
Lời giải
a) Từ giả thiết ta có: \(a \ne 0\) và \(\frac{{a - 4b + 16c}}{a} \le 0 \Rightarrow a(a - 4b + 16c) \le 0 \Rightarrow {(a - 2b)^2} \le 4\left( {{b^2} - 4ac} \right) \Rightarrow \Delta \ge 0\)
do đó phương trình đã cho có 2 nghiệm \({x_1}\,,\,{x_2}\) mà \({x_1}\, + {x_2} = - \frac{b}{a}\) và \({x_1}\,.{x_2} = \frac{c}{a}\). Đến đây thay vào giả thiết ta thu được: \( - \left( {{x_1} + {x_2}} \right) - 4{x_1}{x_2} \ge \frac{1}{4} \Rightarrow \left( {4{x_1} + 1} \right)\left( {4{x_2} + 1} \right) \le 0\). Nếu \({x_1}\,,\,{x_2}\) đều không âm thì dẫn đến điều vô lý. Do vậy phương trình phải có ít nhất một nghiệm âm.
b) Áp dụng bất đẳng thức Cô – si ta được:
\(\sqrt {1 + 8{a^3}} = \sqrt {(1 + 2a)\left( {1 - 2a + 4{a^2}} \right)} \le \frac{{1 + 2a + 1 - 2a + 4{a^2}}}{2} = 2{a^2} + 1.\)
Tương tự, ta có: \(\sqrt {1 + 8{b^3}} \le 2{b^2} + 1;\sqrt {1 + 8{c^3}} \le 2{c^2} + 1.\)
Do đó: \(P \ge \frac{{{a^2}}}{{\left( {2{a^2} + 1} \right)\left( {2{b^2} + 1} \right)}} + \frac{{{b^2}}}{{\left( {2{b^2} + 1} \right)\left( {2{c^2} + 1} \right)}} + \frac{{{c^2}}}{{\left( {2{c^2} + 1} \right)\left( {2{a^2} + 1} \right)}}\)
Tiếp theo ta chứng minh: \(\frac{{{a^2}}}{{\left( {2{a^2} + 1} \right)\left( {2{b^2} + 1} \right)}} + \frac{{{b^2}}}{{\left( {2{b^2} + 1} \right)\left( {2{c^2} + 1} \right)}} + \frac{{{c^2}}}{{\left( {2{c^2} + 1} \right)\left( {2{a^2} + 1} \right)}} \ge \frac{1}{3}(*)\)
Thật vậy: \((*) \Leftrightarrow 3\left( {2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right) + {a^2} + {b^2} + {c^2}} \right) \ge \left( {2{a^2} + 1} \right)\left( {2{b^2} + 1} \right)\left( {2{c^2} + 1} \right)\)
\( \Leftrightarrow 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right) + \left( {{a^2} + {b^2} + {c^2}} \right) \ge 9.\)
Điều này hiển nhiên đúng do \({a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2} \ge 3\sqrt[4]{{{a^4}{b^4}{c^4}}} = 3\) và \({a^2} + {b^2} + {c^2} \ge 3\sqrt[3]{{{a^2}{b^2}{c^2}}} = 3.\)
Vậy GTNN của \(P = \frac{1}{3}\) đạt tại \(a = b = c = 1\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.