Cho P tự thụ phấn được tỉ lệ F1 như sau: 6 hoa kép, màu vàng : 6 hoa đơn, màu vàng : 3 hoa kép, màu tím : 1 hoa đơn, màu tím. Nếu không xảy ra hoán vị gene và tính trạng màu sắc hoa do một cặp gene quy định thì khi cho F1 lai phân tích thu được tỉ lệ kiểu hình như thế nào?
Quảng cáo
Trả lời:
Đáp án
1: 2: 1.
Giải thích
Xét tỉ lệ F1:
Hoa kép/hoa đơn: \(\frac{{6 + 3}}{{6 + 1}} = 9:7\)→ tính trạng do 2 gene phân li độc lập tương tác bổ sung.
Hoa vàng/hoa tím: \(\frac{{6 + 6}}{{3 + 1}} = 3:1\)
→ F1 dị hợp 3 cặp gene
Tích tỉ lệ tính trạng: (9:7)(3:1) ≠ TLKH bài cho nên một trong hai gene quy định tính trạng cánh hoa nằm trên cùng một nhiễm sắc thể với gene quy định tính trạng màu hoa.
Quy ước: A-B-: hoa kép ; A-bb/aaB-/aabb: hoa đơn
D – hoa vàng ; d – hoa tím
F1 có 16 tổ hợp = 4 × 4 → không có hoán vị gene
Giả sử gene A và gene D cùng nằm trên một cặp nhiễm sắc thể tương đồng:
TH1: dị hợp tử đều
P: \(Bb\frac{{AD}}{{ad}} \times Bb\frac{{AD}}{{ad}}\) cho F1 có tỉ lệ kép vàng là 9/16 khác với tỉ lệ của bài (không thỏa mãn).
TH2: dị hợp tử chéo
\(Bb\frac{{Ad}}{{aD}} \times Bb\frac{{Ad}}{{aD}} \to (3B - :1bb)\left( {1\frac{{Ad}}{{Ad}}:2\frac{{Ad}}{{aD}}:1\frac{{aD}}{{aD}}} \right)\) cho tỉ lệ phân li kiểu hình giống bài ra (thỏa mãn).
Cho P lai phân tích
\(Bb\frac{{Ad}}{{aD}} \times bb\frac{{ad}}{{ad}} \to (1Bb:1bb)\left( {1\frac{{Ad}}{{ad}}:1\frac{{aD}}{{ad}}} \right) \to 1Bb\frac{{Ad}}{{ad}}:1Bb\frac{{aD}}{{ad}}:1bb\frac{{Ad}}{{ad}}:1bb\frac{{aD}}{{ad}}\)
Tỉ lệ kiểu hình: 1 kép, tím : 2 đơn, vàng : 1 đơn, tím
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
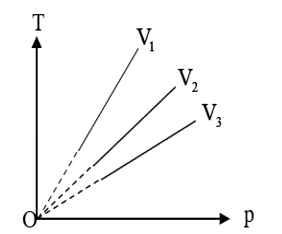
C. V3 < V2 < V1.
Lời giải
Đáp án
V3 < V2 < V1.
Giải thích
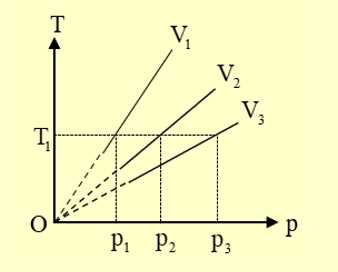
Ứng với nhiệt độ T1 ta có: p1 < p2 < p3
Do nhiệt độ không đổi, áp dụng định luật Boyle, ta có:
\({p_1}{V_1} = {p_2}{V_2} = {p_3}{V_3} \to {V_1} > {V_2} > {V_3}\).
Lời giải
Đáp án
80.
Giải thích
Ta có: \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left[ {3.{{\left( {{3^x}} \right)}^2} + {{2.3}^x} - 1} \right]\left( {{3^x} - y} \right) \le 0\)
\( \Leftrightarrow \left( {{3^x} + 1} \right)\left( {{{3.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left( {{3^{x + 1}} - 1} \right)\left( {{3^x} - y} \right) \le 0\) (do \({3^x} + 1 > 0,\forall x\)).
TH1. \({3^{x + 1}} - 1 \le 0 \Rightarrow x + 1 \le 0 \Leftrightarrow x \le - 1\) ta có \({3^x} - y \ge 0 \Rightarrow y \le {3^x} \le {3^{ - 1}} = \frac{1}{3}\) (vô lý vì \(y\) là số nguyên dương).
TH2. \({3^{x + 1}} - 1 \ge 0 \Rightarrow x + 1 \ge 0 \Leftrightarrow x \ge - 1\) ta có \({3^x} - y \le 0 \Rightarrow y \ge {3^x} \ge {3^{ - 1}} = \frac{1}{3}\) (luôn đúng vì \(y\) là số nguyên dương).
Để ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn bất phương trình nên nghiệm \(x\) chỉ nằm trong khoảng \(\left\{ { - 1;0;1;2;3} \right\} \Rightarrow y < {3^4} = 81\).
Vậy có 80 số nguyên dương \(y\) thỏa mãn yêu cầu đề bài.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.