Logical thinking and problem solving: Choose A, B C or D to answer each question.
Which of the following statements about a book can be a fact?
Logical thinking and problem solving: Choose A, B C or D to answer each question.
Which of the following statements about a book can be a fact?
Quảng cáo
Trả lời:
Đáp án
The book was published in 2018.
Giải thích
Câu nào dưới đây về một cuốn sách có thể là một sự thật?
A. Cuốn sách này là một câu chuyện hấp dẫn không thể bỏ qua.
B. Cuốn sách này được xuất bản vào năm 2018.
C. Cuốn sách này có bìa đẹp nhất.
D. Cuốn sách này là tác phẩm đầy cảm hứng nhất của tác giả.
Giải thích: Câu B là sự thật có thể kiểm chứng vì nó liên quan đến ngày phát hành của sách, trong khi các câu khác là ý kiến chủ quan.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
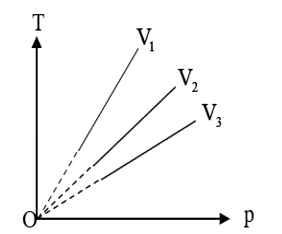
C. V3 < V2 < V1.
Lời giải
Đáp án
V3 < V2 < V1.
Giải thích
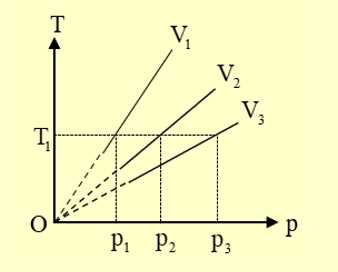
Ứng với nhiệt độ T1 ta có: p1 < p2 < p3
Do nhiệt độ không đổi, áp dụng định luật Boyle, ta có:
\({p_1}{V_1} = {p_2}{V_2} = {p_3}{V_3} \to {V_1} > {V_2} > {V_3}\).
Lời giải
Đáp án
80.
Giải thích
Ta có: \(\left( {{3^{2x + 1}} + {{2.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left[ {3.{{\left( {{3^x}} \right)}^2} + {{2.3}^x} - 1} \right]\left( {{3^x} - y} \right) \le 0\)
\( \Leftrightarrow \left( {{3^x} + 1} \right)\left( {{{3.3}^x} - 1} \right)\left( {{3^x} - y} \right) \le 0 \Leftrightarrow \left( {{3^{x + 1}} - 1} \right)\left( {{3^x} - y} \right) \le 0\) (do \({3^x} + 1 > 0,\forall x\)).
TH1. \({3^{x + 1}} - 1 \le 0 \Rightarrow x + 1 \le 0 \Leftrightarrow x \le - 1\) ta có \({3^x} - y \ge 0 \Rightarrow y \le {3^x} \le {3^{ - 1}} = \frac{1}{3}\) (vô lý vì \(y\) là số nguyên dương).
TH2. \({3^{x + 1}} - 1 \ge 0 \Rightarrow x + 1 \ge 0 \Leftrightarrow x \ge - 1\) ta có \({3^x} - y \le 0 \Rightarrow y \ge {3^x} \ge {3^{ - 1}} = \frac{1}{3}\) (luôn đúng vì \(y\) là số nguyên dương).
Để ứng với mỗi số \(y\) có không quá 5 số nguyên \(x\) thỏa mãn bất phương trình nên nghiệm \(x\) chỉ nằm trong khoảng \(\left\{ { - 1;0;1;2;3} \right\} \Rightarrow y < {3^4} = 81\).
Vậy có 80 số nguyên dương \(y\) thỏa mãn yêu cầu đề bài.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.