1) Giải phương trình \[\left( {x - 2} \right)\left( {x + 1} \right)\left( {x + 3} \right)\left( {x + 6} \right) + 56 = 0\].
2) Giải hệ phương trình \[\left\{ \begin{array}{l}{x^2} + {y^2} = 5\\\left( {x + 1} \right)\left( {y + 1} \right) = 6\end{array} \right.\].
1) Giải phương trình \[\left( {x - 2} \right)\left( {x + 1} \right)\left( {x + 3} \right)\left( {x + 6} \right) + 56 = 0\].
2) Giải hệ phương trình \[\left\{ \begin{array}{l}{x^2} + {y^2} = 5\\\left( {x + 1} \right)\left( {y + 1} \right) = 6\end{array} \right.\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
1) Cách 1: Viết lại phương trình thành \[\left( {x - 2} \right)\left( {x + 6} \right)\left( {x + 1} \right)\left( {x + 3} \right) + 56 = 0 \Leftrightarrow \left( {{x^2} + 4x - 12} \right)\left( {{x^2} + 4x + 3} \right) + 56 = 0\]. |
|
Đặt \[t = {x^2} + 4x - 12\], ta có \[t\left( {t + 15} \right) + 56 = 0 \Leftrightarrow {t^2} + 15t + 56 = 0\]. Ta có \(\Delta = {15^2} - 4.1.56 = 1\) Do đó phương trình trên có nghiệm \[\left[ \begin{array}{l}t = - 7\\t = - 8\end{array} \right.\]. |
|
Với \[t = - 7\] thì \[{x^2} + 4x - 12 = - 7 \Leftrightarrow {x^2} + 4x - 5 = 0\]. Giải tương tự trên, ta được \[\left[ \begin{array}{l}x = 1\\x = - 5\end{array} \right.\]. |
|
Với \[t = - 8\] thì \[{x^2} + 4x - 12 = - 8 \Leftrightarrow {x^2} + 4x - 4 = 0\]. Giải tương tự trên, ta được \[\left[ \begin{array}{l}x = - 2 + 2\sqrt 2 \\x = - 2 - 2\sqrt 2 \end{array} \right.\]. Tập nghiệm của phương trình là \[S = \left\{ {1;\, - 5;\, - 2 + 2\sqrt 2 ;\, - 2 - 2\sqrt 2 } \right\}\]. |
|
Cách 2: Khai triển và thu gọn, ta được \[{x^4} + 8{x^3} + 7{x^2} - 36x + 20 = 0\]. |
|
\[\begin{array}{l} \Leftrightarrow {x^4} - {x^3} + 9{x^3} - 9{x^2} + 16{x^2} - 16x - 20x + 20 = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + 9{x^2} + 16x - 20} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + 5{x^2} + 4{x^2} + 20x - 4x - 20} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right)\left( {{x^2} + 4x - 4} \right) = 0\end{array}\]. |
|
\[ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 5 = 0\\{x^2} + 4x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 5\\{\left( {x + 2} \right)^2} = 8\end{array} \right.\]. |
|
Tập nghiệm của phương trình là \[S = \left\{ {1;\, - 5;\, - 2 + 2\sqrt 2 ;\, - 2 - 2\sqrt 2 } \right\}\]. |
|
2) Cách 1: Đặt \[\left\{ \begin{array}{l}S = x + y\\P = xy\end{array} \right.\]. Hệ phương trình trở thành \[\left\{ \begin{array}{l}{S^2} - 2P = 5\\S + P = 5\end{array} \right.\]. |
|
\[ \Leftrightarrow \left\{ \begin{array}{l}{S^2} - 2\left( {5 - S} \right) = 5\\P = 5 - S\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{S^2} + 2S - 15 = 0 & \left( * \right)\\P = 5 - S\end{array} \right.\]. Phương trình (*) có \(\Delta ' = {1^2} + 1.15 = 16\) nên \[\left[ \begin{array}{l}S = - 5,\,\,P = 10\\S = 3,\,\,P = 2\end{array} \right.\]. |
|
Với \[\left\{ \begin{array}{l}S = - 5\\P = 10\end{array} \right.\] thì \[x,\,\,y\] là hai nghiệm của phương trình \[{X^2} + 5X + 10 = 0\] (phương trình vô nghiệm). |
|
Với \[\left\{ \begin{array}{l}S = 3\\P = 2\end{array} \right.\] thì \[x,\,\,y\] là hai nghiệm của phương trình \[{X^2} - 3X + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}X = 1\\X = 2\end{array} \right.\] (vì \(a + b + c = 1 - 3 + 2 = 0\)). Vậy hệ phương trình có hai nghiệm là \[\left( {1;\,\,2} \right)\] và \[\left( {2;\,\,1} \right)\]. |
|
Cách 2: Từ phương trình sau suy ra \[x \ne - 1,y \ne - 1\] và \[y = \frac{{5 - x}}{{x + 1}}\]. Thế vào phương trình đầu, ta được \[{x^2} + {\left( {\frac{{5 - x}}{{x + 1}}} \right)^2} = 5\]. |
|
\[\begin{array}{l} \Leftrightarrow {x^2}{\left( {x + 1} \right)^2} + {\left( {5 - x} \right)^2} = 5{\left( {x + 1} \right)^2}\\ \Leftrightarrow {x^4} + 2{x^3} - 3{x^2} - 20x + 20 = 0\end{array}\]. |
|
\[\begin{array}{l} \Leftrightarrow \left( {{x^4} - 2{x^3} + 2{x^2}} \right) + \left( {5{x^3} - 15{x^2} + 10x} \right) + \left( {10{x^2} - 30x + 20} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 3x + 2} \right)\left( {{x^2} + 5x + 10} \right) = 0\end{array}\]. |
|
\[ \Leftrightarrow {x^2} - 3x + 2 = 0\] (vì với mọi \[x\]). \[ \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 2\\x = 2 \Rightarrow y = 1\end{array} \right.\]. |
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
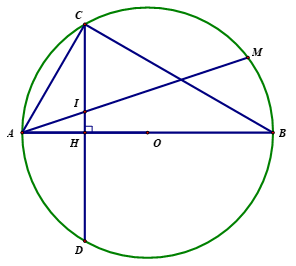
Vì \[H\] là trung điểm của \[OA\] nên \(AH = \frac{{OA}}{2} = \frac{R}{2} \cdot \) Ta có \[\widehat {ACB} = {90^0}\] (góc nội tiếp chắn nửa đường tròn). Xét tam giác \(ABC\) vuông tại \(C\) có đường cao \(CH\): \(A{C^2} = AB.AH = 2R.\frac{R}{2} = {R^2} \Rightarrow AC = R\). |
|
\(B{C^2} = A{B^2} - A{C^2} = 4{R^2} - {R^2} = 3{R^2} \Rightarrow BC = R\sqrt 3 .\) |
|
\(CH.AB = AC.BC \Rightarrow CH = \frac{{AC.BC}}{{AB}} = \frac{{R.R\sqrt 3 }}{{2R}} = \frac{{R\sqrt 3 }}{2} \cdot \) |
|
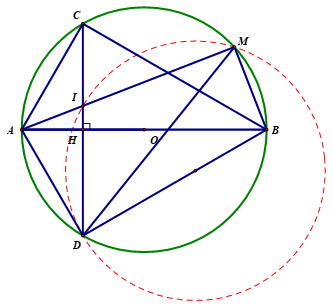
Cách 1: Tam giác \(ABD\) vuông tại \(D\) đường cao \(DH\) ta có \(A{D^2} = AH.AB.\) \[\Delta AIH\] và \[\Delta ABM\] có góc \[A\] chung và \[\widehat {AHI} = \widehat {AMB}\left( { = {{90}^0}} \right)\].
|
|
|
Do đó \(A{D^2} = AI.AM \Rightarrow \frac{{AD}}{{AM}} = \frac{{AI}}{{AD}} \cdot \) |
|
|
\[\Delta ADI\]
Suy ra \(\Delta ADI\) \(\Delta AMD\) (c.g.c). |
|
|
Vậy \(\widehat {ADI} = \widehat {AMD}\). Do đó \(AD\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta IDM\). |
|
|
Cách 2: \[OA\] là đường trung trực của \[CD\] nên \[AC = AD\]. |
|
|
Tam giác \[ACD\] cân tại \[A\] nên \[\widehat {ACD} = \widehat {ADI}\]. |
|
|
Mặt khác \[\widehat {ACD} = \widehat {AMD}\] (cùng chắn cung \[AD\]). |
|
|
Vậy \(\widehat {ADI} = \widehat {AMD}\). Do đó \(AD\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta IDM\). |
|
|
Tìm vị trí điểm \(M\) trên cung nhỏ \(BC\) sao cho \(MB + MC + MD\) đạt giá trị lớn nhất. |
|
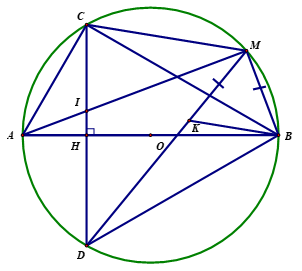 Ta có \(CD = 2.CH = 2.\frac{{R\sqrt 3 }}{2} = R\sqrt 3 \). |
|
|
Mặt khác \(\Delta BCD\) cân tại \(B\) nên \(BD = BC = R\sqrt 3 \). Vậy \(\Delta BCD\) là tam giác đều. Trên đoạn \[MD\] lấy điểm \[K\] sao cho \[MK = MB\]. \(\Delta MBK\) cân tại \(M\) có \(\widehat {BMK} = \widehat {BCD} = {60^0}\) nên là tam giác đều. |
|
|
Ta có \[\widehat {CBM} + \widehat {CBK} = {60^0},\,\,\widehat {DBK} + \widehat {CBK} = {60^0}\]. Dẫn đến \[\widehat {CBM} = \widehat {DBK}\]. Xét \(\Delta CBM\) và \[\Delta DBK\] có: \(CB = DB,\,\widehat {\,CBM} = \widehat {DBK},\,\,BM = BK\). Do đó \(\Delta CBM = \Delta DBK \Rightarrow MC = KD\). Vậy \(MD = MK + KD = MB + MC\). |
|
|
Ta có \(MB + MC + MD = 2MD \le 4R\). Vậy \(MB + MC + MD\) đạt giá trị lớn nhất khi \(MD\) là đường kính của đường tròn \(\left( O \right)\). Do đó \(M\) là điểm chính giữa của cung nhỏ \(BC\). |
Lời giải
Chia hình vuông đã cho thành 49 hình vuông nhỏ bằng nhau, mỗi hình vuông có cạnh bằng \[\frac{1}{7}\].
Theo nguyên lý Dirichlet tồn tại một hình vuông nhỏ \[ABCD\] chứa ít nhất 3 điểm.
Gọi \[O\] là giao điểm của \[AC\] và \[BD\]. Bán kính đường tròn ngoại tiếp \[ABCD\] là \[r = \frac{{AB}}{{\sqrt 2 }} = \frac{1}{{7\sqrt 2 }}\].
Ta thấy \[\frac{1}{{7\sqrt 2 }} < \frac{1}{9}\]. Vậy 3 điểm đó nằm trong hình tròn tâm \[O\] bán kính \[R = \frac{1}{9}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập