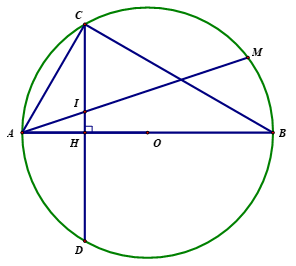
Cho đường tròn tâm \(O\) đường kính \(AB = 2R\). Gọi \(H\) là trung điểm của \(OA\). Vẽ dây \(CD\) vuông góc với \(AB\) tại \(H\). Gọi \(M\) là một điểm di động trên cung nhỏ \(BC\) (\(M\) không trùng với \(B\) và \(C\)), \(AM\) cắt \(CD\) tại \(I\).
1) Tính độ dài các đoạn thẳng \(AC,\,\,BC,\,\,CH\) theo \(R\).
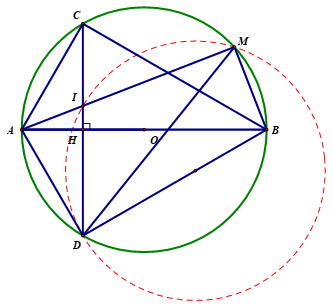
2) Chứng minh \(AD\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(IDM\).
3) Tìm vị trí điểm \(M\) trên cung nhỏ \(BC\) sao cho \(MB + MC + MD\) đạt giá trị lớn nhất.
Cho đường tròn tâm \(O\) đường kính \(AB = 2R\). Gọi \(H\) là trung điểm của \(OA\). Vẽ dây \(CD\) vuông góc với \(AB\) tại \(H\). Gọi \(M\) là một điểm di động trên cung nhỏ \(BC\) (\(M\) không trùng với \(B\) và \(C\)), \(AM\) cắt \(CD\) tại \(I\).
1) Tính độ dài các đoạn thẳng \(AC,\,\,BC,\,\,CH\) theo \(R\).
2) Chứng minh \(AD\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(IDM\).
3) Tìm vị trí điểm \(M\) trên cung nhỏ \(BC\) sao cho \(MB + MC + MD\) đạt giá trị lớn nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Vì \[H\] là trung điểm của \[OA\] nên \(AH = \frac{{OA}}{2} = \frac{R}{2} \cdot \) Ta có \[\widehat {ACB} = {90^0}\] (góc nội tiếp chắn nửa đường tròn). Xét tam giác \(ABC\) vuông tại \(C\) có đường cao \(CH\): \(A{C^2} = AB.AH = 2R.\frac{R}{2} = {R^2} \Rightarrow AC = R\). |
|
\(B{C^2} = A{B^2} - A{C^2} = 4{R^2} - {R^2} = 3{R^2} \Rightarrow BC = R\sqrt 3 .\) |
|
\(CH.AB = AC.BC \Rightarrow CH = \frac{{AC.BC}}{{AB}} = \frac{{R.R\sqrt 3 }}{{2R}} = \frac{{R\sqrt 3 }}{2} \cdot \) |
|
Cách 1: Tam giác \(ABD\) vuông tại \(D\) đường cao \(DH\) ta có \(A{D^2} = AH.AB.\) \[\Delta AIH\] và \[\Delta ABM\] có góc \[A\] chung và \[\widehat {AHI} = \widehat {AMB}\left( { = {{90}^0}} \right)\].
|
|
|
Do đó \(A{D^2} = AI.AM \Rightarrow \frac{{AD}}{{AM}} = \frac{{AI}}{{AD}} \cdot \) |
|
|
\[\Delta ADI\]
Suy ra \(\Delta ADI\) \(\Delta AMD\) (c.g.c). |
|
|
Vậy \(\widehat {ADI} = \widehat {AMD}\). Do đó \(AD\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta IDM\). |
|
|
Cách 2: \[OA\] là đường trung trực của \[CD\] nên \[AC = AD\]. |
|
|
Tam giác \[ACD\] cân tại \[A\] nên \[\widehat {ACD} = \widehat {ADI}\]. |
|
|
Mặt khác \[\widehat {ACD} = \widehat {AMD}\] (cùng chắn cung \[AD\]). |
|
|
Vậy \(\widehat {ADI} = \widehat {AMD}\). Do đó \(AD\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta IDM\). |
|
|
Tìm vị trí điểm \(M\) trên cung nhỏ \(BC\) sao cho \(MB + MC + MD\) đạt giá trị lớn nhất. |
|
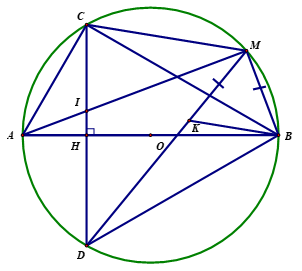 Ta có \(CD = 2.CH = 2.\frac{{R\sqrt 3 }}{2} = R\sqrt 3 \). |
|
|
Mặt khác \(\Delta BCD\) cân tại \(B\) nên \(BD = BC = R\sqrt 3 \). Vậy \(\Delta BCD\) là tam giác đều. Trên đoạn \[MD\] lấy điểm \[K\] sao cho \[MK = MB\]. \(\Delta MBK\) cân tại \(M\) có \(\widehat {BMK} = \widehat {BCD} = {60^0}\) nên là tam giác đều. |
|
|
Ta có \[\widehat {CBM} + \widehat {CBK} = {60^0},\,\,\widehat {DBK} + \widehat {CBK} = {60^0}\]. Dẫn đến \[\widehat {CBM} = \widehat {DBK}\]. Xét \(\Delta CBM\) và \[\Delta DBK\] có: \(CB = DB,\,\widehat {\,CBM} = \widehat {DBK},\,\,BM = BK\). Do đó \(\Delta CBM = \Delta DBK \Rightarrow MC = KD\). Vậy \(MD = MK + KD = MB + MC\). |
|
|
Ta có \(MB + MC + MD = 2MD \le 4R\). Vậy \(MB + MC + MD\) đạt giá trị lớn nhất khi \(MD\) là đường kính của đường tròn \(\left( O \right)\). Do đó \(M\) là điểm chính giữa của cung nhỏ \(BC\). |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Do vai trò của \[x,\,\,y\] đối xứng nhau nên giả sử \[x \le y\]. Với \[z = 0\] thì \[{x^2} + {y^2} = 36\]. (1) Vì \[x \le y\] nên \[{x^2} \le 18 \Rightarrow 0 \le x \le 4\]. Thử trực tiếp, ta được \[\left\{ \begin{array}{l}x = 0\\y = 6\end{array} \right.\] thỏa (1). |
|
Với \[z \ge 1\]: Do \[2023 \vdots 7,\,\,35 \vdots 7\] nên \[{x^2} + {y^2} \vdots 7\]. (2) Đặt \[x = 7a + r,\,\,y = 7b + t\] với \[a,\,\,b,\,\,r,\,\,t\] là các số tự nhiên thỏa\[0 \le r \le 6,\,\,0 \le t \le 6\]. Khi đó \[{x^2} + {y^2} = 49{a^2} + 14ar + 49{b^2} + 14bt + {r^2} + {t^2}\]. (3) Từ (2) và (3) suy ra \[{r^2} + {t^2} \vdots 7\]. Thử trực tiếp, ta thấy chỉ có \[r = 0,\,\,t = 0\] thỏa mãn. Do đó \[x = 7a,\,\,y = 7b\]. |
|
Thay vào phương trình ban đầu: \[49{a^2} + 49{b^2} = {2023^z} + 35 \Leftrightarrow 7\left( {{a^2} + {b^2}} \right) = {289^z}{.7^{z - 1}} + 5\]. Nếu \[z > 1\] ta có vế trái chia hết cho 7 và vế phải không chia hết cho 7 (vô lý). Nếu \[z = 1\] ta có: \[7\left( {{a^2} + {b^2}} \right) = 289 + 5 \Leftrightarrow {a^2} + {b^2} = 42\]. |
|
Dễ dàng kiểm tra được phương trình \[{a^2} + {b^2} = 42\] không có nghiệm tự nhiên. Vậy phương trình ban đầu có hai nghiệm \[\left\{ \begin{array}{l}x = 0\\y = 6\\z = 0\end{array} \right.,\left\{ \begin{array}{l}x = 6\\y = 0\\z = 0\end{array} \right.\]. |
Lời giải
Chia hình vuông đã cho thành 49 hình vuông nhỏ bằng nhau, mỗi hình vuông có cạnh bằng \[\frac{1}{7}\].
Theo nguyên lý Dirichlet tồn tại một hình vuông nhỏ \[ABCD\] chứa ít nhất 3 điểm.
Gọi \[O\] là giao điểm của \[AC\] và \[BD\]. Bán kính đường tròn ngoại tiếp \[ABCD\] là \[r = \frac{{AB}}{{\sqrt 2 }} = \frac{1}{{7\sqrt 2 }}\].
Ta thấy \[\frac{1}{{7\sqrt 2 }} < \frac{1}{9}\]. Vậy 3 điểm đó nằm trong hình tròn tâm \[O\] bán kính \[R = \frac{1}{9}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập