Cho các số thực \[a,\,\,b,\,\,c\] thỏa mãn \(a > b > c;\,\,ab + bc + ca > 0\) và \(a + b + c = 1\).
Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{1}{{a - b}} + \frac{1}{{b - c}} + \frac{1}{{a - c}} + \frac{5}{{2\sqrt {ab + bc + ca} }}\).
Cho các số thực \[a,\,\,b,\,\,c\] thỏa mãn \(a > b > c;\,\,ab + bc + ca > 0\) và \(a + b + c = 1\).
Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{1}{{a - b}} + \frac{1}{{b - c}} + \frac{1}{{a - c}} + \frac{5}{{2\sqrt {ab + bc + ca} }}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta sử dụng các bất đẳng thức \(\frac{1}{m} + \frac{1}{n} \ge \frac{4}{{m + n}} \ge \frac{{2\sqrt 2 }}{{\sqrt {{m^2} + {n^2}} }}\) với \(m > 0;n > 0\)
Dấu bằng xảy ra khi \(m = n\)
\(P = \frac{1}{{a - b}} + \frac{1}{{b - c}} + \frac{1}{{a - c}} + \frac{5}{{2\sqrt {ab + bc + ca} }}\)
\(P \ge \frac{4}{{a - c}} + \frac{1}{{a - c}} + \frac{5}{{2\sqrt {ab + bc + ca} }} = \frac{5}{{a - c}} + \frac{5}{{2\sqrt {ab + bc + ca} }}\)
Lại có: \(\frac{5}{{a - c}} + \frac{5}{{2\sqrt {ab + bc + ca} }} \ge 5\frac{{2\sqrt 2 }}{{\sqrt {{{(a - c)}^2} + 4(ab + bc + ca)} }} = \frac{{10\sqrt 2 }}{{\sqrt {{{(a + c)}^2} + 4b(a + c)} }}\)
\( \Rightarrow P \ge \frac{{10\sqrt 2 }}{{\sqrt {(a + c)(a + c + 4b)} }} = \frac{{10\sqrt 2 }}{{\sqrt {(1 - b)(1 + 3b)} }}\,\,\,\,\left( {do\,\,a + c = 1 - b} \right)\)
\( \Rightarrow P \ge \frac{{10\sqrt 6 }}{{\sqrt {\left( {3 - 3b} \right)\left( {1 + 3b} \right)} }} \ge \frac{{10\sqrt 6 }}{{\frac{{3 - 3b + 1 + 3b}}{2}}} = 5\sqrt 6 \)
Giá trị nhỏ nhất của P bằng \(5\sqrt 6 \) khi
\(\left\{ \begin{array}{l}a > b > c\\a + b + c = 1\\a - b = b - c\\a - c = 2\sqrt {b(a + c) + ca} \\3 - 3b = 1 + 3b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > b > c\\b = \frac{1}{3}\\a + c = \frac{2}{3}\\a - c = 2\sqrt {\frac{2}{9} + ca} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{{2 + \sqrt 6 }}{6}\\b = \frac{1}{3}\\c = \frac{{2 - \sqrt 6 }}{6}\end{array} \right.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
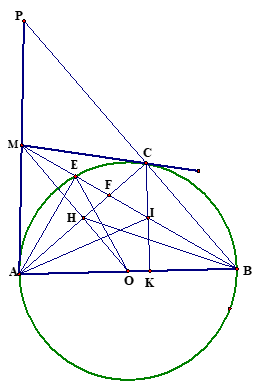
a) Ta có \(ME.MB = M{A^2}\) do \(\Delta MAB\) vuông tại A có đường cao AE.
Lại có \(MH.MO = M{A^2}\) do \(\Delta MAO\) vuông tại A có đường cao AH.
\( \Rightarrow ME.MB = MH.MO\)
\( \Rightarrow \frac{{ME}}{{MH}} = \frac{{MO}}{{MB}}\)\[ \Rightarrow \Delta OME \sim \Delta BMH\]
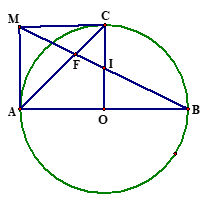
b) Ta có\(MA = MC,\,\,OA = OC\) suy ra đường thẳng \(MO\)là trung trực đoạn thẳng \(AC\)nên \(MO \bot AC\). Kéo dài \(BC\) cắt \(AM\) tại \(P\) nên \(MO//PB\)\( \Rightarrow M\) trung điểm \(AP.\)
Ta có \(\frac{{IC}}{{MP}} = \frac{{BI}}{{BM}}\) và \(\frac{{IK}}{{MA}} = \frac{{BI}}{{BM}}\)\( \Rightarrow \frac{{IC}}{{MP}} = \frac{{IK}}{{MA}} \Rightarrow IC = IK\)
Suy ra \(I\) trung điểm của đoạn thẳng \(CK\).
\( \Rightarrow {S_{\Delta ACI}} = \frac{1}{2}{S_{\Delta ACK}};{S_{\Delta BCI}} = \frac{1}{2}{S_{\Delta BCK}}\,\, \Rightarrow {S_{\Delta AIC}} + {S_{\Delta BCI}} = \frac{1}{2}{S_{\Delta ABC}}\, = \frac{1}{4}CK.AB\)
Do đoạn thẳng \(AB\)không đổi nên tổng diện tích hai tam giác \(IAC\) và \(IBC\)lớn nhất. lớn nhất khi \(C\) điểm chính giữa hay \(K\) trùng tâm \(O.\)
Khi đó tứ giác\(AOCM\) là hình vuông.
\( \Rightarrow \frac{{FI}}{{FM}} = \frac{{IC}}{{AM}} = \frac{1}{2} \Rightarrow FI = \frac{1}{3}IM = \frac{1}{6}BM.\) Lại có \(B{M^2} = A{B^2} + M{A^2} = \frac{{5A{B^2}}}{4}\)
\( \Rightarrow BM = \frac{{AB\sqrt 5 }}{2} \Rightarrow \frac{{FI}}{{AB}} = \frac{1}{6}.\frac{{\frac{{AB\sqrt 5 }}{2}}}{{AB}} = \frac{{\sqrt 5 }}{{12}}.\)
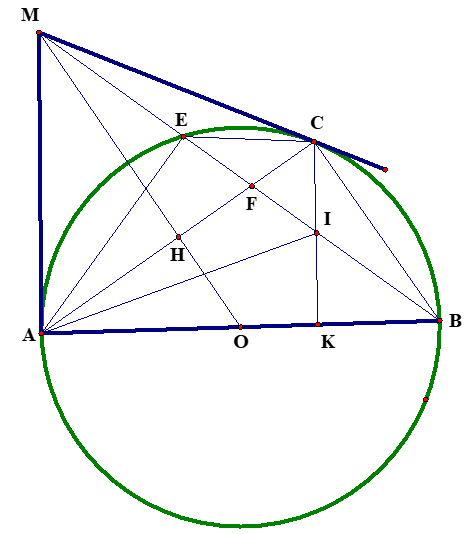
.c) Ta có
\[\Delta MEC \sim \Delta MCB \Rightarrow \frac{{ME}}{{MC}} = \frac{{CE}}{{CB}}\]
\[\Delta MEA \sim \Delta MAB \Rightarrow \frac{{MA}}{{MB}} = \frac{{EA}}{{AB}}\]
\[ \Rightarrow \frac{{ME}}{{MC}}.\frac{{MA}}{{MB}} = \frac{{CE}}{{CB}}.\frac{{EA}}{{AB}} \Rightarrow \frac{{ME}}{{MB}} = \frac{{CE}}{{CB}}.\frac{{AE}}{{AB}}\,\,(1).\]
.Mặt khác
\[\Delta FEC \sim \Delta FAB \Rightarrow \frac{{FE}}{{FA}} = \frac{{CE}}{{AB}}\]
\[\Delta FAE \sim \Delta FBC \Rightarrow \frac{{FA}}{{FB}} = \frac{{AE}}{{BC}}\]
\[ \Rightarrow \frac{{FE}}{{FA}}.\frac{{FA}}{{FB}} = \frac{{CE}}{{AB}}.\frac{{EA}}{{CB}} \Rightarrow \frac{{FE}}{{FB}} = \frac{{CE}}{{CB}}.\frac{{AE}}{{AB}}\,\,(2).\]
Từ (1) và (2) \[ \Rightarrow \frac{{ME}}{{MB}} = \frac{{FE}}{{FB}}\,\,\]
\[ \Rightarrow \frac{{MB - EB}}{{MB}} = \frac{{EB - FB}}{{FB}}\,\, \Rightarrow 1 - \frac{{EB}}{{MB}} = \frac{{EB}}{{FB}} - 1 \Rightarrow 2 = \,\frac{{EB}}{{MB}} + \frac{{EB}}{{FB}}\]
\[ \Rightarrow 2 = EB\left( {\frac{1}{{MB}} + \frac{1}{{FB}}} \right) \Rightarrow \frac{1}{{BM}} + \frac{1}{{BF}} = \frac{2}{{BE}}\] (ĐPCM).
Lời giải
ĐK: \(11 - 4(x - y) \ge 0\)
\((x + 2)(2 - y) = 8 \Leftrightarrow 2\left( {x - y} \right) - xy = 4 \Rightarrow 2\left( {x - y} \right) = 4 + xy\)
Thế vào phương trình (2) ta có:
\(\sqrt {11 - 2(4 + xy)} + {x^2}{y^2} - 3xy + 1 = 0 \Leftrightarrow \sqrt {3 - 2xy} + {x^2}{y^2} - 3xy + 1 = 0\)
\( \Leftrightarrow \left( {\sqrt {3 - 2xy} - 1} \right) + {x^2}{y^2} - 3xy + 2 = 0\)
\( \Leftrightarrow \frac{{2(1 - xy)}}{{\sqrt {3 - 2xy} + 1}} + (1 - xy)(2 - xy) = 0\)\( \Leftrightarrow \left( {1 - xy} \right)\left( {\frac{2}{{\sqrt {3 - 2xy} + 1}} + 2 - xy} \right) = 0\)
\( \Leftrightarrow xy = 1\) (Do \(\frac{2}{{\sqrt {3 - 2xy} + 1}} + 2 - xy > 0,\,\,\,\forall xy \le \frac{3}{2}\))
Ta có: \(\left\{ \begin{array}{l}xy = 1\\2\left( {x - y} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{1}{x}\\2\left( {x - \frac{1}{x}} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{1}{x}\\2{x^2} - 5x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{1}{x}\\x = \frac{{5 \pm \sqrt {41} }}{4}\end{array} \right.\)
Vậy hệ phương trình có nghiệm là:
\(\left( {x;\,\,y} \right) = \left( {\frac{{5 + \sqrt {41} }}{4};\frac{{ - 5 + \sqrt {41} }}{4}} \right)\) và \(\left( {\frac{{5 - \sqrt {41} }}{4};\frac{{ - 5 - \sqrt {41} }}{4}} \right)\)
ĐK: \(\left\{ \begin{array}{l}{x^2} + 3x + 11 \ge 0\\x + 2 \ge 0\end{array} \right. \Leftrightarrow x \ge - 2\)
\(\sqrt {{x^2} + 3x + 11} - \sqrt {x + 2} = 2x - 2 \Leftrightarrow \sqrt {{{(x - 1)}^2} + 5(x + 2)} - \sqrt {x + 2} = 2(x - 1)\)
Xét \[x = - 2\] (không phải là nghiệm)
Xét \[x > - 2\] Chia hai vế phương trình cho\[\sqrt {x + 2} \] ta được:\(\sqrt {\frac{{{{(x - 1)}^2}}}{{x + 2}} + 5} - 1 = \frac{{2(x - 1)}}{{\sqrt {x + 2} }}.\) Đặt \[t = \frac{{x - 1}}{{\sqrt {x + 2} }}\] ta được phương trình:\(\sqrt {{t^2} + 5} - 1 = 2t\)
\( \Leftrightarrow \sqrt {{t^2} + 5} = 2t + 1 \Leftrightarrow \left\{ \begin{array}{l}2t + 1 \ge 0\\{t^2} + 5 = {(2t + 1)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t \ge - \frac{1}{2}\\3{t^2} + 4t - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t \ge - \frac{1}{2}\\t = - 2;\,\,t = \frac{2}{3}\end{array} \right. \Leftrightarrow t = \frac{2}{3}\)
Khi \[t = \frac{2}{3}\] ta được phương trình:\[\frac{{x - 1}}{{\sqrt {x + 2} }} = \frac{2}{3} \Leftrightarrow 2\sqrt {x + 2} = 3(x - 1) \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\4(x + 2) = 9{(x - 1)^2}\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\9{x^2} - 22x + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x = \frac{{11 \pm 4\sqrt 7 }}{9}\end{array} \right. \Leftrightarrow x = \frac{{11 + 4\sqrt 7 }}{9}.\]
Vậy phương trình có đúng 1 nghiệm \[x = \frac{{11 + 4\sqrt 7 }}{9}\]
Chú ý: Học sinh có thể giải theo cách: Đặt \(\left\{ \begin{array}{l}a = x - 1\\b = \sqrt {x + 2} \ge 0.\end{array} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập