Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(d:y = x + m\). Gọi \(S\) là tập hợp các giá trị của \(m\) để \(d\) cắt \(\left( C \right)\) tại 2 điểm phân biệt có hoành độ \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 9\). Tổng các phần tử của tập hợp \(S\) là:
Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}\) có đồ thị \(\left( C \right)\) và đường thẳng \(d:y = x + m\). Gọi \(S\) là tập hợp các giá trị của \(m\) để \(d\) cắt \(\left( C \right)\) tại 2 điểm phân biệt có hoành độ \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 9\). Tổng các phần tử của tập hợp \(S\) là:
Quảng cáo
Trả lời:
Đáp án đúng là B
Phương pháp giải
Biện luận số nghiệm của phương trì̀hh hoành độ giao điểm, ứng dụng định lý Viet
Lời giải
Phương trình hoành độ giao điểm:
\(\frac{{x + 1}}{{x - 1}} = x + m \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{g\left( x \right) = {x^2} + \left( {m - 2} \right)x - m - 1 = 0\left( 1 \right)}\end{array}} \right.\)
Để đồ thị \(\left( C \right)\) cắt \(d\) tại 2 điểm phân biệt \( \Leftrightarrow g\left( x \right) = 0\) có 2 nghiệm phân biệt khác 1.
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{g\left( 1 \right) = - 2 \ne 0}\\{{\rm{\Delta }} = {{(m - 2)}^2} + 4\left( {m + 1} \right) > 0}\end{array}} \right.\) (*)
Khi đó phương trình \(g\left( x \right) = 0\) có hai nghiệm \({x_1},{x_2}\)
Theo định lý Viet ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2 - m}\\{{x_1}.{x_2} = - m - 1}\end{array}} \right.\)
Ta có:
\(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} = {(2 - m)^2} + 2\left( {m + 1} \right) = {m^2} - 2m + 6 = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 3}\\{m = - 1}\end{array}} \right.\) thỏa mãn (*)
Vậy \(S = \left\{ {3; - 1} \right\} \Rightarrow T = 2\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "168"
Phương pháp giải
Ứng dụng tích phân
Lời giải
Quãng đường ô tô đi được từ lúc lăn bánh đến khi được phanh:
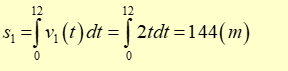
Vận tốc \({v_2}\left( t \right)\left( {m/s} \right)\) của ô tô từ lúc được phanh đến khi dừng hẳn thỏa mãn:
\({v_2}\left( t \right) = \mathop \smallint \nolimits^ - 12dt = - 12t + C\),
\({v_2}\left( {12} \right) = {v_1}\left( {12} \right) = 24 \Rightarrow C = 168 \Rightarrow {v_2}\left( t \right) = - 12t + 168\left( {{\rm{m}}/{\rm{s}}} \right)\)
Thời điểm xe dừng hẳn tương ứng với thỏa mãn \({v_2}\left( t \right) = 0 \Leftrightarrow t = 14\left( s \right)\)
Quãng đường ô tô đi được từ lúc xe được phanh đến khi dừng hẳn là:
\({s_2} = \int\limits_{12}^{14} {{v_2}\left( t \right)dt} = \int\limits_{12}^{14} {\left( { - 12t + 168} \right)dt} = 24m\)
Quãng đường cần tính \(s = {s_1} + {s_2} = 144 + 24 = 168\left( m \right)\)
Câu 2
Lời giải
Đáp án đúng là D
Phương pháp giải
Phân tích đồ thị hình vẽ.
Dựa vào lí thuyết sự chuyển thể của chất.
Lời giải
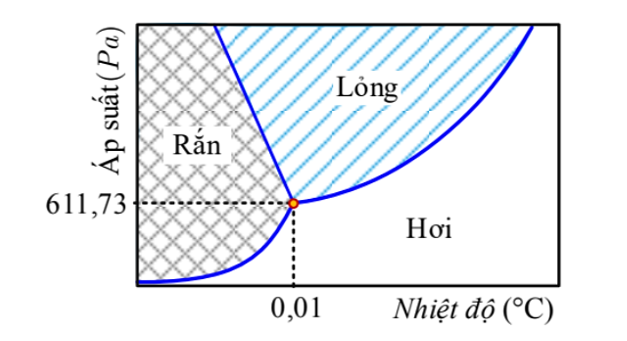
Dựa vào đồ thị trên ta có:
Giữ nguyên áp suất, nếu tăng nhiệt độ hệ chuyển thành thể hơi.
Giữ nguyên áp suất, nếu giảm nhiệt độ, hệ chuyển thành thể rắn.
Giữ nguyên nhiệt độ, tăng áp suất, hệ chuyển thành thể lỏng.
Giữ nguyên nhiệt độ, giảm áp suất, hệ chuyển thành thể hơi.
Vậy đáp án sai là D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. Cách để hình thành nhiều tế bào nơ-ron.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.