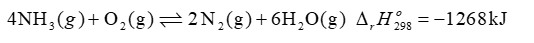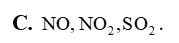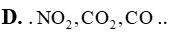Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 20)
92 người thi tuần này 4.6 231 lượt thi 235 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là C
Phương pháp giải
Lập bảng biến thiên của hàm số \(g\left( x \right) = f\left( {x - 2} \right) + \frac{{{x^3}}}{3} - \frac{7}{2}{x^2} + 12x + 1\)
Lời giải
Xét hàm số \(g\left( x \right) = f\left( {x - 2} \right) + \frac{{{x^3}}}{3} - \frac{7}{2}{x^2} + 12x + 1\)
\(g'\left( x \right) = f'\left( {x - 2} \right) + {x^2} - 7x + 12\)
Để hàm số đồng biến :
\( \Rightarrow g'\left( x \right) > 0 \Leftrightarrow f'\left( {x - 2} \right) + {x^2} - 7x + 12 > 0 \Leftrightarrow f'\left( {x - 2} \right) > - {x^2} + 7x - 12\)
\( \Leftrightarrow f'\left( {x - 2} \right) > - \left( {x - 2} \right)\left( {x - 2 - 3} \right) - 2\)
Đặt \(t = x - 2 \Rightarrow f'\left( t \right) > - t\left( {t - 3} \right) - 2 \Leftrightarrow f'\left( t \right) > - {t^2} + 3t - 2\)
Vẽ đồ thị hàm số: \(h\left( t \right) = - {t^2} + 3t - 2\)

Dựa vào tương giao hai đồ thị ta thấy
\(f'\left( t \right) > - {t^2} + 3t - 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a < t < 1,( - 2 < a < - 1)}\\{t > 2}\end{array}} \right.\)
\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{a < x - 2 < 1}\\{x - 2 > 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a + 2 < x < 3}\\{x > 4}\end{array}} \right.} \right.\)
Vậy hàm số đồng biến trên các khoảng \(\left( {a + 2;3} \right),( - 2 < a < - 1)\) và \(\left( {4;7} \right)\).
Lời giải
Đáp án đúng là "14"
Phương pháp giải
phương pháp đổi biến số
Lời giải
Ta có : \(g'\left( x \right) = f'\left( {x - m} \right) - \left( {x - m - 1} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow f'\left( {x - m} \right) = x - m - 1\)
Đặt: \(t = x - m \Rightarrow f'\left( t \right) = t - 1\)
Khi đó nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số \(y = f'\left( t \right)\) và đường thẳng \(y = t - 1\)

Dựa vào đồ thị ta được \(f'\left( t \right) = t - 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = - 1}\\{t = 1}\\{1 = 3}\end{array}} \right.\)
Bảng xét dấu của \(g'\left( t \right)\)

Từ bảng xét dấu ta thấy hàm số \(g\left( t \right)\) đồng biến trên khoảng \(\left( { - 1;1} \right)\) và \(\left( {3; + \infty } \right)\)
Hay: \(\left[ {\begin{array}{*{20}{l}}{ - 1 < t < 1}\\{t > 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 1 < x - m < 1}\\{x - m > 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m - 1 < x < m + 1}\\{x > m + 3}\end{array}} \right.} \right.} \right.\)
Để hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( {5;6} \right)\) thì \(\left[ {\begin{array}{*{20}{l}}{m - 1 \le 5 \le m + 1}\\{m + 3 \le 5 < 6}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{5 \le m \le 6}\\{m \le 2}\end{array}} \right.} \right.\)
Vì \(m\) là các số nguyên dương nên \(S = \left\{ {1;2;5;6} \right\}\)
Vậy tổng tất cả các phần tử của \(S\) là : 14
Câu 3
Lời giải
Đáp án đúng là D
Phương pháp giải
Dựa vào bảng xét dấu của đạo hàm
Lời giải
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;2} \right)\)
Câu 4
Lời giải
Đáp án đúng là A
Phương pháp giải
Đặt \(t = {\rm{tan}}x\), khảo sát hàm số nhận được
Lời giải
Đặt \(t = {\rm{tan}}x\), vì \(x \in \left( {0;\frac{\pi }{4}} \right) \Rightarrow t \in \left( {0;1} \right)\)
Xét hàm số: \(f\left( t \right) = \frac{{t - 2}}{{t - m}}\forall t \in \left( {0;1} \right)\). Tập xác định: \(D = \mathbb{R}\backslash \left\{ m \right\}\)
Ta có\(:f'\left( t \right) = \frac{{2 - m}}{{{{(t - m)}^2}}}\)
Để hàm số \(y\) đồng biến trên khoảng \(\left( {0;\frac{\pi }{4}} \right) \Leftrightarrow f'\left( t \right) > 0\forall t \in \left( {0;1} \right)\)
\( \Leftrightarrow \frac{{2 - m}}{{{{(t - m)}^2}}} > 0\forall t \in \left( {0;1} \right)\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 - m > 0}\\{m \notin \left( {0;1} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 2}\\{\left[ {\begin{array}{*{20}{c}}{m \le 0}\\{m \ge 1}\end{array}{\rm{\;}}} \right.}\end{array} \Leftrightarrow m \in \left( { - \infty ;0\left] \cup \right[1;2} \right)} \right.} \right.\)
Lời giải
Đáp án đúng là C
Phương pháp giải
Xác định tọa độ cực trị, viết phương trình đường thẳng đi qua hai điểm cực trị
Lời giải
Ta có: \(y' = 3{x^2} - 6mx,y' = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2m}\end{array}} \right.\)
Đồ thị \(\left( C \right)\) luôn có hai điểm cực trị với mọi \(m\) nguyên dương (vì \(m\) là số nguyên dương nên phương trình \(y' = 0\) luôn có hai nghiệm phân biệt).
Khi đó \(A\left( {0;4{m^2} - 2} \right),B\left( {2m; - 4{m^3} + 4{m^2} - 2} \right)\)
\( \Rightarrow AB = \sqrt {4{m^2} + 16{m^6}} = 2\left| m \right|\sqrt {4{m^4} + 1} \)
Phương trình đường thẳng \(AB\):
\(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} \Rightarrow \frac{{x - 0}}{{2m - 0}} = \frac{{y - \left( {4{m^2} - 2} \right)}}{{ - 4{m^3}}} \Leftrightarrow 2{m^2}x + y - 4{m^2} + 2 = 0\)
Thay tọa độ điểm \(C\) vào phương trình đường thẳng \(AB\), dễ thấy điểm \(C \notin AB\)
\(d\left( {C,AB} \right) = \frac{{\left| {2{m^2} + 4 - 4{m^2} + 2} \right|}}{{\sqrt {4{m^4} + 1} }} = \frac{{2\left| {{m^2} - 3} \right|}}{{\sqrt {4{m^4} + 1} }}\)
\( \Rightarrow {S_{\Delta ABC}} = \frac{1}{2}AB.d\left( {C,AB} \right) = 4 \Leftrightarrow \frac{1}{2}.2.\left| m \right|\sqrt {4{m^4} + 1} .\frac{{2\left| {{m^2} - 3} \right|}}{{\sqrt {4{m^4} + 1} }} = 4\)
\( \Leftrightarrow \left| {m\left( {{m^2} - 3} \right)} \right| = 2 \Leftrightarrow {m^6} + 9{m^2} - 4 = 0\)
\( \Leftrightarrow {\left( {{m^2} - 1} \right)^2}\left( {{m^2} - 4} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = \pm 1}\\{m = \pm 2}\end{array}} \right.\)
Do \(m\) nguyên dương nên ta nhận được \(m \in \left\{ {1;2} \right\}\)
Ñ Học sinh nên kiểm tra điều kiện để hàm số có hai điểm cực trị và điều kiện để ba điểm \(A,B,C\) không thẳng hàng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
D. \(I\left( { - 2;2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 43
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 45
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
B. âm mưu/ tình yêu
C. thế lực/ trạng thái
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
B. môi trường/ khoa học
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
B. Bâng khuâng, lưu luyến
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
B. Không quan tâm đến cộng đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
B. Âm điệu
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
B. Trân trọng, lên án
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
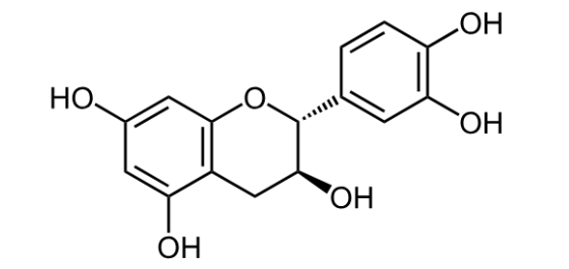
B. cellulose, β-glucose.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 115
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 117
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
B. xuất cư và tử vong.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 127
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
B. dreamt
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
B. postpone/ build
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 151
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 152
D. Sure, I'll do it now.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 153
B. The popcorn was great.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 154
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 155
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 157
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 158
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 159
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 160
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 161
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 162
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 163
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 164
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 165
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 166
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 167
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 168
B. Wow, the colors you’re using are fantastic! Could I try adding some too?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 169
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 170
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 171
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 172
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Giả sử \(5{\rm{\% }}\) email của bạn nhận được là email rác. Bạn sử dụng một hệ thống lọc email rác mà khả năng lọc đúng email rác của hệ thống này là \(95{\rm{\% }}\) và có \(10{\rm{\% }}\) những email không phải là email rác nhưng vẫn bị lọc
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 174
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 175
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 176
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Thực ra, trừ một số trường hợp đặc biệt, não trẻ em sinh ra hầu hết đều không có sự chênh lệch quá lớn về các tế bào nơ-ron, sự khác nhau giữa các tế bào nơ-ron sẽ thể hiện rõ nhất khi chúng trưởng thành: “Hệ thống dày đặc tế bào nơ-ron được liên kết bởi các sợi trục trong não, bắt đầu phát triển trong giai đoạn cuối của thai nhi và lớn lên mạnh mẽ sau khi trẻ được sinh ra”. Lúc này, não của trẻ em có cấu tạo nơ-ron rất phức tạp, tương đương não của một thiên tài. Nhưng sự phát triển tế bào nơ-ron chỉ tiếp diễn cho đến sau khi sinh mười tháng tuổi, từ đó sẽ giảm dần và trở lại bình thường cho đến năm sáu tuổi. Đây cũng là giai đoạn phản ứng gây ra sự khác nhau đặc trưng giữa chúng ta và thiên tài. Có thể hiểu rằng, có càng nhiều các tế bào liên kết nơ-ron càng tốt, muốn có nhiều liên kết giữa các nơ-ron, cần cho trẻ càng nhiều tác nhân kích thích đến năm giác quan, trẻ sẽ dung nạp được đa dạng nguồn thông tin. Điều này định ước rằng, từ lúc lọt lòng cho đến sáu tuổi là một quãng thời gian đặc biệt quan trọng trong quá trình phát triển chung và bên trong mỗi đứa trẻ đều tiềm ẩn khả năng vô hạn. Việc của chúng ta là làm sao, để đánh thức được những thiên tánh đã sẵn có trong người mỗi trẻ.
(Trần Huy Toàn, Tinh hoa giáo dục – di sản cho muôn đời sau, NXB Khoa học và Kĩ thuật, Hà Nội, 2021)
Câu 177
B. Cách để hình thành nhiều tế bào nơ-ron.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 178
B. Trẻ sơ sinh dưới 10 tháng tuổi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 179
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 180
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 181
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Khoa học và công nghệ góp phần thúc đẩy cuộc cách mạng thời trang vì môi trường
(1) Thời trang nhanh là thuật ngữ được sử dụng để mô tả những món quần áo bắt kịp xu hướng nhanh; chúng lấy ý tưởng từ những món đồ trong các buổi trình diễn thời trang và được sản xuất rất nhanh để chuyển đến các cửa hàng. Những năm trở lại đây, thời trang nhanh ngày càng trở nên phổ biến vì giá cả phải chăng, đa dạng về mẫu mã, được cập nhật liên tục và thịnh hành. Người tiêu dùng, đặc biệt là giới trẻ, ngày càng ưa chuộng những phong cách mới, từ đó kích thích sức mua, khiến ngành công nghiệp thời trang nhanh ngày càng phát triển và có chỗ đứng vững chắc trong lòng người tiêu dùng, đặc biệt trong thời đại của cuộc Cách mạng công nghiệp 4.0 khi người trẻ dành nhiều thời gian để mua sắm quần áo giá rẻ trên các sàn thương mại điện tử. Sự ra đời của thời trang nhanh đi kèm với giá cả phải chăng đã thu hút khách hàng chi tiêu một lượng tiền lớn để có thể sử dụng chúng. […]
(2) Sự phát triển nhanh chóng và mạnh mẽ của thời trang nói chung và thời trang nhanh nói riêng đã tàn phá môi trường theo rất nhiều cách. Để có được sản phẩm quần áo màu sắc rực rỡ, chất liệu bắt mắt, phần lớn các công ty phải nhờ vào hóa chất độc hại. Nước nhuộm vải chính là thứ gây ô nhiễm nguồn nước nhiều thứ hai toàn cầu. Chất liệu polyester là loại vải được sử dụng phổ biến nhất trong ngành công nghiệp may mặc. Loại vải này được giặt trong máy giặt gia đình tạo nên những sợi vải siêu nhỏ (microfiber), dễ dàng đi qua nhà máy xử lý nước thải vào các tuyến đường thủy, không phân hủy được, làm gia tăng lượng nhựa trong nước biển, chúng chính là mối đe dọa nghiêm trọng đối với sinh vật dưới nước. […]
(3) Sau giai đoạn Covid-19, người tiêu dùng có xu hướng hướng tới thời trang bền vững. Điều này đã khiến những người sáng tạo thời trang như nhà thiết kế, nhà phát triển sản phẩm, người mua và người bán hàng lựa chọn các sản phẩm thay thế thời trang bền vững và thân thiện với môi trường. Việc tái sử dụng, tái chế hàng may mặc và phụ kiện sẽ trở nên phổ biến hơn trong tương lai. Vì hiện tại trên thị trường dệt may có chưa đến 10% nguyên liệu tái chế, nên các khoản đầu tư trong toàn ngành sẽ được yêu cầu để mở rộng quy trình và công nghệ tái chế theo chu trình khép kín để giảm thiểu tác động đến môi trường. […]
(4) Từ xưa, các sản phẩm da thuộc luôn mang lại vẻ đẹp sang trọng và thời thượng, giúp nâng tầm đẳng cấp thời trang cho người mặc. Tuy nhiên, chất liệu này tác động xấu tới môi trường như ô nhiễm không khí (khí thải metan từ động vật) cũng như làm cạn kiệt tài nguyên rừng (phá rừng để tăng diện tích đất chăn nuôi). Vì vậy, một số công ty thời trang đã tạo ra một quá trình sản xuất da thuộc mà không cần phải sát hại động vật. Nhờ vào việc nuôi cấy collagen - protein được tìm thấy trong da động vật, các công ty đã phát triển chúng thành da nhân tạo, chất liệu này có thể ngăn ngừa được sự tàn phá của ngành thời trang đối với môi trường hiện nay.
(5) Tại Ý, với gần 1 triệu tấn vỏ cam, quýt được thải ra môi trường mỗi năm, một cặp đôi người Ý đã sử dụng vỏ cam, quýt dư thừa để chế biến chúng thành vải. Cách hoạt động của phương pháp này chính là chiết xuất xenlulozo từ vỏ cam, biến nó thành sợi polyme và dệt thành vải. Một thương hiệu đồ da nổi tiếng của Ý là Salvatore Ferragamo cũng đã lần đầu tiên sử dụng chất liệu vải dệt từ vỏ cam. Loại sợi chiết xuất từ vỏ cam được dệt thành loại vải có tính chất không thua kém cotton hay lụa, thậm chí còn có thể dùng làm vải dệt kim. Đây được xem là cách giúp các nhà sản xuất trái cây giải quyết được phần nào vấn đề xử lý rác thải và hướng tới sự thân thiện với môi trường.
(6) Về phía các công dân trên toàn cầu, nếu thực sự mong muốn trở thành người tiêu dùng thông thái, góp phần chung tay giảm thiểu tác hại của thời trang nhanh đến môi trường, mọi người đều có thể tham khảo một số gợi ý như: lựa chọn các thương hiệu thời trang bền vững; ưu tiên chất lượng thay vì số lượng; quyên góp hoặc bán quần áo đã qua sử dụng; trao đổi quần áo với bạn bè, người thân, tái chế quần áo cũ thành các vật dụng hữu ích khác…
(Nguyễn Hằng, Tạp chí Khoa học và Công nghệ, số ra ngày 27-03-2023)
Câu 182
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 183
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 184
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 185
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 186
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 187
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Như vậy, với rất nhiều hình thức văn bản từ kể vè đến miêu tả, từ vài câu khuyên răn đến những lời đối đáp, đồng dao đã dạy trẻ nói năng qua các mẫu câu sinh động. Cách dạy này rất phù hợp với phát triển năng lực ngôn ngữ – cũng như dạy các kỹ năng lao động khác – rất tự nhiên, hợp với tâm lý lứa tuổi. Trong thực tế, hoạt động nói năng của người bình thường cũng như các nghệ nhân diễn xướng với năng lực sử dụng ngôn ngữ bậc cao, cách dạy, cách học qua thực hành ấy đã chứng tỏ có hiệu quả. Các mẫu mực, các vẻ đẹp ngôn ngữ cả về âm thanh, nhịp điệu lẫn khuôn hình thể loại nhập vào trẻ rất tự nhiên, rất ngọt ngào. Đó là con đường cần tham khảo để tránh sự lý tính hóa theo hướng trang bị kiến thức ngôn ngữ học quá khó, quá sớm. Đồng dao với những bài vè, bài ru em, bài hát vui chơi cũng đem lại cho trẻ vốn hiểu biết nhiều mặt về thiên nhiên, xã hội, con người. Rất có thể các trí thức bình dân cũng ý thức được việc cung cấp vốn sống, vốn hiểu biết qua những bài hát trẻ con này. Cái cách làm mà sau này ta gọi là “lồng ghép” kiến thức sử địa vào bài tập đọc cho trẻ tiểu học có thể thấy rõ ở nhiều bài đồng dao.
(Lê Xuân Mậu, Đồng dao dạy trẻ những gì?, In trong Văn học dân gian – Cái hay, vẻ đẹp, NXB Lao động, Hà Nội, 2012)
Câu 188
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 189
B. Hình thức phong phú
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 190
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 191
B. Củng cố từ vựng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 192
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Tôi sinh ra từ cọng rơm vàng
Từ bùn tối, cánh đồng và ngọn sóng
Từ những cơn gió mặn
Thổi rộng dài tít tắp những triền đê.
Nơi tôi nằm râm mát bóng lùm tre
Bước chân trâu thậm thịch trưa hè
Tiếng gà ban mai, đêm trăng chó sủa
Thành nước mắt, thịt da và hơi thở.
Có thể quên được chăng
Có thể chối từ điều đó?
Đất chôn nhau cũng có quyền lìa bỏ
Như thói quen xé đi tờ lịch cũ
Như thói quen?
Đất lạ quê người trong cơn sốt miên man
Trước mắt tôi những cọng rơm vàng...
(Trịnh Thanh Sơn, Cọng rơm vàng, dẫn theo thivien.net)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 194
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 195
B. Khơi gợi cảm xúc
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 196
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 197
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Sáng hôm sau. Hắn thức dậy trên cái giường nhà hắn. Hắn thấy mình mẩy đau như dần, đầu nặng, miệng khô và đắng. Cổ thì ráo và rát cháy. Hắn đưa tay với ấm nước ở trên bàn để uống. Ấm nước đầy và nước hãy còn ấm. Đó là sự ý tứ của Từ. Hộ hiểu thế, và lòng buồn nao nao. Bởi hắn lờ mờ nhớ ra rằng: hình như đêm qua hắn say rượu, đi la cà chán rồi về, lại gây sự với Từ; hình như hắn lại đánh cả Từ đuổi Từ đi rồi mới đóng cửa lại và đi ngủ... Hắn đột nhiên hoảng sợ, nhổm dậy, mắt nhớn nhác tìm Từ. Nhưng không! Từ vẫn còn nhà... Chắc hẳn trong lúc quá say, hắn gài cửa nhưng chưa gài được, thành thử khi thấy hắn ngủ mệt rồi Từ lại bế con vào. Bây giờ Từ đang thiếp đi trên võng, đứa con nhỏ nằm bên. Từ vốn dậy sớm quen. Sáng nay, chắc Từ mệt quá, vừa mới lịm đi nên mới ngủ trưa như thể. Đầu Từ ngoẹo về một bên. Một tay Từ trật ra ngoài mép võng, sã xuống, cái bàn tay hơi xoè ra lỏng lẻo. Dáng nằm thật là khó nhọc và khổ não. Hắn bùi ngùi. Chao ôi! Trông Từ nằm thật đáng thương! Hèn chi mà Từ khổ cả một đời người! Cái tướng vất vả lộ ra cả đến trong giấc ngủ. Hộ nhớ ra rằng: một đôi lúc, nếu nhìn kĩ thì Từ khó mặt lắm. Đột nhiên Hộ nảy ra ý muốn lại gần Từ, nhìn kĩ xem mặt Từ lúc bây giờ ra sao ? Hắn rón rén, đi chân không lại. Hắn ngồi xổm ngay xuống đất, bên cạnh võng và cố thở cho thật khẽ. Hắn ngắm nghía mặt Từ lâu lắm. Da mặt Từ xanh nhợt; môi nhợt nhạt; mi mắt hơi tim tím và xung quanh mắt có quầng, đôi má đã hơi hóp lại khiến mặt hơi có cạnh. Hộ khẽ thở dài và lắc đầu ái ngại. Hắn dịu dàng nắm lấy tay sẽ xuống của Từ. Cái bàn tay lủng củng rặt những xương! Trên mu bàn tay, những đường gân xanh bóng ra làn da mỏng và xanh trong, xanh lọc. Cái cổ tay mỏng mảnh. Tất cả lộ một cái gì mềm yếu, một cái gì ẻo lả, cần được hắn che chở và bênh vực... một vẻ bạc mệnh, một cái gì đau khổ và chật vật, cần được hắn vỗ về an ủi... Thế mà hắn đã làm gì để cho đời Từ đỡ khổ hơn? Hắn đã làm gì để cho Từ khỏi khổ? Nước mắt hắn bật ra như nước một quả chanh mà người ta bóp mạnh. Và hắn khóc... Ôi chao! Hắn khóc! Hắn khóc nức nở, khóc như thể không ra tiếng khóc. Hắn ôm chặt lấy cái bàn tay bé nhỏ của Từ vào ngực mình mà khóc. Từ thức dậy, Từ hiểu ngay, không cần hỏi một câu nào cũng hiểu. Và Từ cảm động. Mắt Từ giàn giụa nước. Từ khể rút tay ra, vòng lên cổ chồng, nhẹ nhàng níu hắn vào, để hắn gục đầu lên cạnh ngực Từ. Hắn lại càng khóc to hơn và cố nói qua tiếng khóc:
– Anh... anh... chỉ là... một thằng... khốn nạn !...
– Không !... Anh chỉ là một người khổ sở !... Chính vì em mà anh khổ...
Từ bảo thể. Tay Từ níu mạnh hơn một chút. Ngực Từ thổn thức. Từ chực ngả đầu sát vào vai Hộ. Nhưng đứa con, bị giằng, khóc thét lên. Từ vội buồng chồng ra để vỗ con. Tiếng vẫn còn ướt lệ, Từ dỗ nó :
− A! Mợ đây! Mợ đây mà! Ôi chao! Con tôi nó giật mình... Mợ thương...
Hộ đã tránh chỗ để Từ đưa võng... Từ vừa đưa, vừa hát:
Ai làm cho khói lên giời,
Cho mưa xuống đất, cho người biệt li
Ai làm cho Nam, Bắc phân kì,
Cho hai hàng lệ đầm đìa tấm thân...
(Nam Cao, Đời thừa, Nam Cao - Tác phẩm, tập II, NXB Văn học, Hà Nội, 1977)
Câu 198
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 199
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 200
C. Ngôi thứ ba toàn tri
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 201
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 202
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 7
Bốn bóng đèn giống hệt nhau K, L, M và N được mắc vào mạch điện như hình:
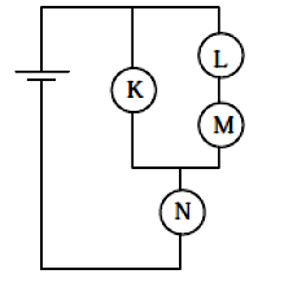
Câu 203
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 204
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 205
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 8
Nitrogen phân tử (N2) sử dụng nhiều trong công nghệ bảo quản chống oxi hoá và là chất làm lạnh phổ biến. Chất này cũng được sử dụng trong sản xuất các linh kiện điện tử, sản xuất thép không gỉ, bơm vào lốp ô tô và máy bay, sử dụng trong các thiết bị làm lạnh, sử dụng làm nguồn làm mát để tăng tốc CPU, GPU hay các dạng phần cứng khác,… Máy tạo khí nitrogen được sử dụng cho ngành công nghiệp thực phẩm như đóng gói sản phẩm, đóng chai, lưu trữ rượu, nước, sữa, dầu; cho ngành y tế và công nghệ hoá chất, công nghệ cắt laser, hàn đặc biệt là trong các ứng dụng mà có yếu tố cháy nổ, khí oxygen sẽ được thay thế bằng nitrogen.
Bên cạnh những ứng dụng quan trọng trên thì đối với một số ngành khí nitrogen quả là kẻ thù. Những người thợ lặn kinh nghiệm có thể ước lượng chiều sâu bằng cảm giác. Khi lặn sâu người ta có cảm giác bàng hoàng, cử động mất tự nhiên như say rượu vậy. Trạng thái đó được gọi là “say nitrogen” bởi thủ phạm chính là nitrogen. Khi thợ lặn càng xuống sâu thì không khí họ thở càng bị nén mạnh. Độ tan của khí nitrogen trong máu tăng lên gây trạng thái "say nitrogen".
Câu 206
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 207
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 208
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 9
Đột biến gene là những thay đổi trong trình tự DNA của một sinh vật, có thể xảy ra một cách tự nhiên hoặc do tác động của con người. Những đột biến này có thể dẫn đến các biến đổi về chức năng của protein hoặc thậm chí gây ra các bệnh di truyền. Tuy nhiên, khi được nghiên cứu và áp dụng đúng cách, đột biến gene có thể mang lại nhiều lợi ích lớn lao trong lĩnh vực khoa học và y học.
Trong nông nghiệp, người ta đã sử dụng đột biến gene để cải thiện giống cây trồng. Bằng cách tạo ra các đột biến có lợi, các nhà khoa học có thể giúp cây trồng kháng lại sâu bệnh, tăng năng suất, hoặc cải thiện khả năng chịu đựng các điều kiện bất lợi như hạn hán và độ mặn cao. Đột biến gene đã góp phần quan trọng vào việc nâng cao chất lượng và số lượng sản phẩm nông nghiệp trên thế giới.
Trong y học, công nghệ chỉnh sửa gene dựa trên các phương pháp như CRISPR-Cas9 đã tạo ra một bước đột phá lớn. Phương pháp này cho phép các nhà khoa học "sửa chữa" những đoạn gene bị đột biến gây bệnh trong cơ thể, mở ra hy vọng cho việc điều trị các bệnh di truyền như bệnh xơ nang, bệnh máu khó đông và nhiều bệnh khác. Không chỉ dừng lại ở việc điều trị bệnh, đột biến gene còn được áp dụng trong nghiên cứu tạo ra các mô hình động vật biến đổi gene để thử nghiệm thuốc và phát triển liệu pháp điều trị mới.
Bên cạnh những lợi ích, ứng dụng của đột biến gene cũng đặt ra nhiều thách thức và câu hỏi về đạo đức. Việc sử dụng công nghệ chỉnh sửa gene để thay đổi các đặc tính di truyền của con người, đặc biệt là những đặc điểm không liên quan đến bệnh tật như ngoại hình hay trí tuệ, có thể gây ra những tranh cãi về sự can thiệp vào tự nhiên và quyền tự do của con người.
Câu 209
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 210
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 211
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 10
Kenedy coi Việt Nam là tuyến cuối cùng chống cộng sản ở khu vực Đông Nam Á và nếu Mĩ rút khỏi Việt Nam thì sự sụp đổ sẽ diễn ra ở cả khu vực Đông Nam Á! Ngày 8-5-1961, chính sách đối với Việt Nam đã chính thức được phê chuẩn và mang tên NSAM-52 với nội dung chủ yếu: Tăng cường và mở rộng quyền điều hành tác chiến, chỉ huy yểm hộ của phái đoàn cố vấn quân sự MAAG; đưa lực lượng đặc biệt của Mĩ vào miền Nam Việt Nam, giúp Diệm xây dựng lực lượng đặc biệt, chốt chặt biên giới, chống miền Bắc xâm nhập; tăng cường mở rộng, cải tiến trang bị và huấn luyện quân đội, coi đó là công cụ chủ yếu để chống chiến tranh du kích; khẩn trương bình định, lập ấp chiến lược hòng dồn hơn 10 triệu người dân miền Nam vào các trại tập trung trá hình để thực hiện “Tát nước bắt cá”, cô lập để tiêu diệt cách mạng miền Nam; ra sức củng cố chính quyền các cấp và đẩy mạnh các hoạt động chiến tranh phá hoại miền Bắc.
(Theo Đại cương lịch sử Việt Nam, tập 3)
Câu 212
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 213
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 214
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 11
Cuộc khủng hoảng 1929-1933 chẳng những tàn phá nền kinh tế mà còn gây ra những hậu quả nặng nề về mặt chính trị và xã hội cho CNTB. Trong cuộc khủng hoảng này số công nhân thất nghiệp nên đến 50 triệu. Hàng triệu người mất nhà cửa vì không trả được tiền cầm cố. Hàng triệu nông dân bị mất ruộng đất, sống trong cảnh nghèo đói. Công nhân không được trả lương, ở nhiều nước không có bảo hiểm xã hội và thất nghiệp không được phụ cấp, hoặc ở mức độ ít ỏi không thể đảm bảo nhu cầu tối thiểu của gia đình nghèo khổ. Trong bối cảnh đó, phong trào cách mạng thế giới đã có bước chuyển mới: thoái trào tiến dần lên cao trào. Hàng ngàn cuộc biểu tình và những cuộc đi bộ của những người thất nghiệp trong nhiều trường hợp đã xung đột với cảnh sát và quân đội; đấu tranh bãi công chống việc hạ thấp tiền lương đã nổ ra ở hầu khắp các nước. Theo thống kê không đầy đủ, trong thời gian từ năm 1928 đến cuối năm 1933, số người tham gia bãi công ở các nước TBCN đã lên tới 17 triệu, còn số ngày bãi công là 267 triệu.
(Theo lịch sử thế giới hiện đại, trang 99)
Câu 215
B. Cuộc khủng hoảng 1933-1945.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 216
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 217
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 12
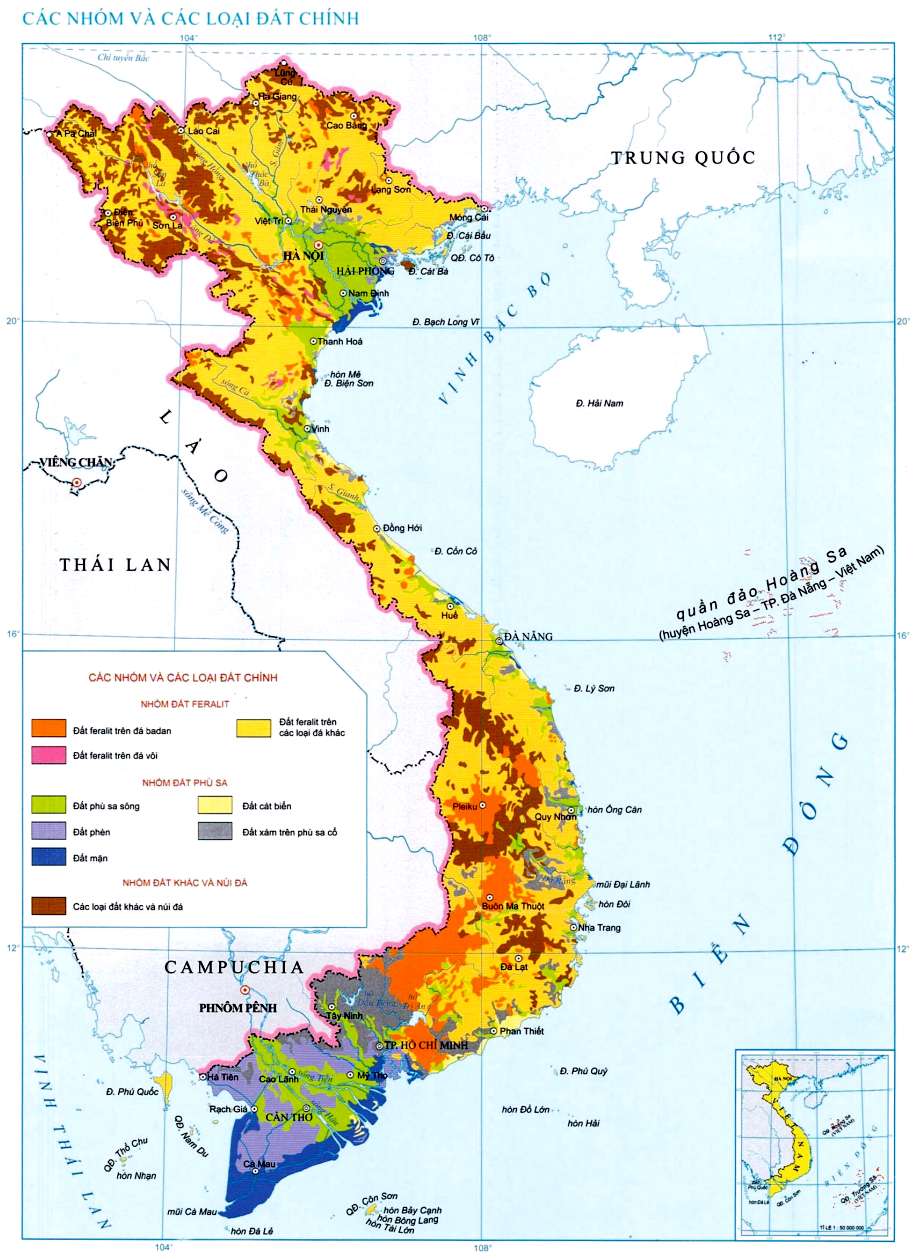
(Atlat Địa lí Việt Nam, Nxb Giáo dục Việt Nam, 2024)
Câu 218
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 219
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 220
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 13
The last two decades have seen enormous changes in the way people's lives are affected by IT. Twenty years ago, few people had (631) ________ to a computer while today most people use them at work, home or school and use of e-mail and the Internet is an everyday event.
These developments have brought many benefits to our lives. E-mail makes communication much easier and more immediate. This has numerous benefits for business, commerce, and education. The World Wide Web means that information on every conceivable subject is now available to us. Clearly, for many people this has (632) ______and more convenient.
However, not all the effects of the new technology have been (633)__________. Many people feel that the widespread use of e-mail is destroying traditional forms of communication such as letter writing, telephone and face-to-face conversation. With ever increasing use of information technology, these negative elements are likely to increase in the future.
In addition, the huge size of the Web means it is almost impossible to control and regulate. This has led to (634) _________. Yet perhaps the biggest threat to IT in years to come will be the computer virus -more sophisticated or more destructive strains are almost inevitable.
In conclusion, developments in IT have brought many benefits, yet I believe (635) ______ in the future are likely to produce many negative effects that will need to be addressed very carefully.
Câu 221
D. chance
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 222
B. made life much easier
D. to make much easier life
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 223
D. beneficial
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 224
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 225
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 14
The incredible growth of the Internet over recent years has caused problems for parents and teachers. Parents worry about which sites their children spend time on, who they chat to online and the possible effects that computer games might have on them. For teachers, meanwhile, the main worry is the way the Internet makes cheating easier!
Schools and universities say there has been a huge increase in plagiarism – taking other people’s words and ideas and pretending that they are your own. In the past, anyone who wanted to copy had to go to a library, find the right books, read through them, find the sections they needed and then physically write down the words they wanted to use. Nowadays, though, students can simply copy extracts from websites- while really desperate students sometimes copy whole essays! As if this wasn’t bad enough, sites offering to actually do homework – at a price – have also started appearing.
Despite all this, we shouldn’t assume that the Internet only brings problems. Indeed, you could say that for every problem the Internet creates, it also brings a solution. Parents can now use sophisticated controls to stop kids accessing sites that might do them harm, while new software helps teachers to detect copied work immediately. Many, of course, are already able to recognize when someone is cheating! “Some students suddenly start using words they can’t possibly understand like dialectical antagonism”, explains one teacher, “or parts of their essays feel different.”
One of the hardest things for teachers today is deciding how to mix modern technology with traditional study skills – and how best to use the Web in class. As more and more schools install computers in every classroom, the role of the teacher is changing. Making sure students don’t just copy things and do learn how to quote copied work properly is part of their job, but so is designing suitable projects to fully exploit the Web in helping students learn about subjects and develop their life and social skills.
(Adapted from Pre-Intermediate Outcomes by Hugh Della $ Andrew Walkley)Câu 226
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 227
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 228
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 229
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 230
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 15
Being aware of one's own emotions - recognizing and acknowledging feelings as they happen - is at the very heart of Emotional Intelligence. And this awareness encompasses not only moods but also thoughts about those moods. People who are able to monitor their feelings as they arise are less likely to be ruled by them and are thus better able to manage their emotions.
Managing emotions does not mean suppressing them; nor does it mean giving free rein to every feeling. Psychologist Daniel Goleman, one of several authors who have popularized the notion of Emotional Intelligence, insisted that the goal is balance and that every feeling has value and significance. As Goleman said, "A life without passion would be a dull wasteland of neutrality, cut off and isolated from the richness of life itself." Thus, we manage our emotions by expressing them in an appropriate manner. Emotions can also be managed by engaging in activities that cheer us up, soothe our hurts, or reassure us when we feel anxious.
Clearly, awareness and management of emotions are not independent. For instance, you might think that individuals who seem to experience their feelings more intensely than others would be less able to manage them. However, a critical component of awareness of emotions is the ability to assign meaning to them - to know why we are experiencing a particular feeling or mooD. Psychologists have found that, among individuals who experience intense emotions, individual differences in the ability to assign meaning to those feelings predict differences in the ability to manage them. In other words, if two individuals are intensely angry, the one who is better able to understand why he or she is angry will also be better able to manage the anger.
Self-motivation refers to strong emotional self-control, which enables a person to get moving and pursue worthy goals, persist at tasks even when frustrated, and resist the temptation to act on impulse. Resisting impulsive behavior is, according to Goleman, "the root of all emotional self- control."
Of all the attributes of Emotional Intelligence, the ability to postpone immediate gratification and to persist in working toward some greater future gain is most closely related to success - whether one is trying to build a business, get a college degree, or even stay on a diet. One researcher examined whether this trait can predict a child's success in school. The study showed that 4-year-old children who can delay instant gratification in order to advance toward some future goal will be “far superior as students” when they graduate from high school than will 4-year-olds who are not able to resist the impulse to satisfy their immediate wishes.
Câu 231
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 232
B. We should ignore some feelings.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 233
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 234
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 235
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.