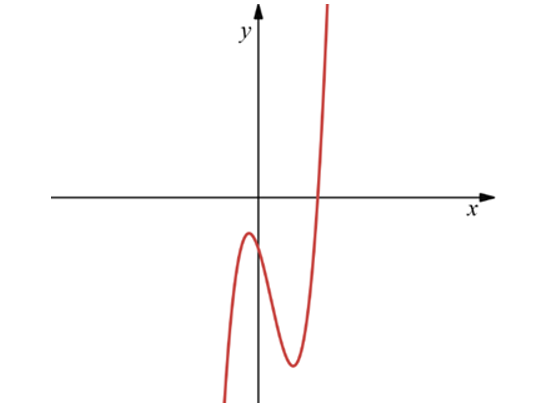
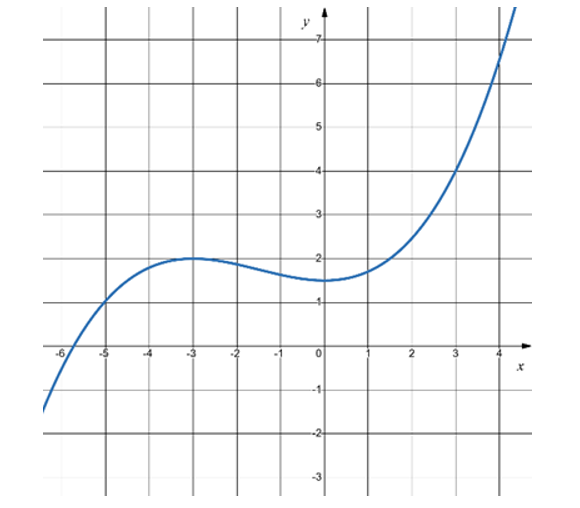
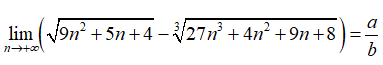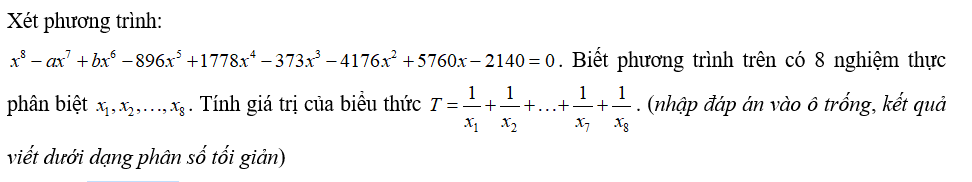Bộ 41 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 23)
64 người thi tuần này 4.6 225 lượt thi 235 câu hỏi 120 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là C
Phương pháp giải
Xem lại cách xác định mệnh đề phủ định.
Lời giải
Cách xác định mệnh đề phủ định: Thay dấu ∀ thành dấu ∃ và ngược lại, đồng thời đối với mệnh đề cuối cùng không đi cùng dấu ∀ và ∃, lấy mệnh đề phủ định của mệnh đề đó.
Sử dụng phương pháp trên, ta xác định được mệnh đề phủ định của mệnh đề đã cho là 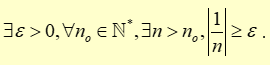
Câu 2
Lời giải
Đáp án đúng là B
Phương pháp giải
Đưa về hệ bất phương trình bậc nhất hai ẩn.
Lời giải
Gọi số kg nước trái cây loại I và loại II mà tiệm sẽ sản xuất trong một ngày lần lượt là \(x,y\left( {x,y \ge 0} \right)\).
Khi đó, lượng táo, cam và dứa mà cửa hàng sẽ sử dụng lần lượt là \(2x + 3y,\,\,x + 4y,\,\,4x + y\left( {{\rm{kg}}} \right)\).
Do trong một ngày, cửa hàng đó có thể sử dụng tối đa 120 kg táo, 120 kg cam và 150 kg dứa, nên ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0,y \ge 0}\\{2x + 3y \le 120}\\{x + 4y \le 120}\\{4x + y \le 150}\end{array}} \right.\).
Khi đó, biểu diễn hệ bất phương trình trên trên hệ toạ độ \(Oxy\), ta được miền nghiệm của hệ là miền đa giác với các đỉnh \(O\left( {0;0} \right),A\left( {0;30} \right),B\left( {24;24} \right),C\left( {33;18} \right),D\left( {37,5;0} \right)\).
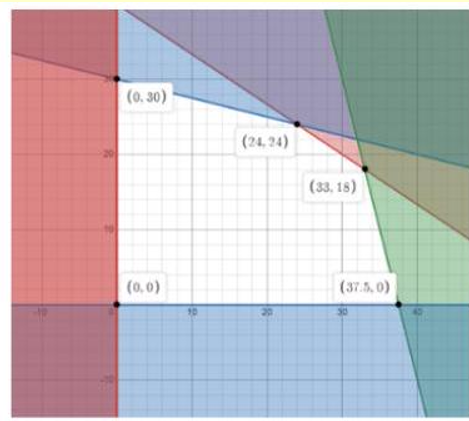
Lợi nhuận của quán trong một ngày sẽ là \(L\left( {x;y} \right) = 70000\left( {x + y} \right)\) (đồng).
\(\begin{array}{l}L\left( O \right) = 0\\L\left( A \right) = 70000\left( {0 + 30} \right) = 2100000\\L\left( B \right) = 70000\left( {24 + 24} \right) = 3360000\\L\left( C \right) = 70000\left( {33 + 18} \right) = 3570000\\L\left( D \right) = 70000\left( {37,5 + 0} \right) = 2625000\end{array}\)
Khi đó, ta xác định được lợi nhuận tối đa của quán trong một ngày là 3570000 đồng khi lựa chọn sản xuất 33 kg nước loại I và 18 kg nước loại II.
Câu 3
Lời giải
Đáp án đúng là B
Phương pháp giải
Sử dụng các phương trình tính độ dài đáy và chiều cao của tam giác.
Lời giải
Phương trình đường thẳng \(AB\) đi qua \(A\left( {3;4} \right)\) nhận \(\overrightarrow {AB} \left( { - 1;1} \right)\) làm vectơ chỉ phương là \(1\left( {x - 3} \right) + 1\left( {y - 4} \right) = 0 \Leftrightarrow x + y - 7 = 0\).
Khoảng cách từ điểm \(C\) tới đường thẳng \(AB\) là \(d\left( {C;AB} \right) = \frac{{\left| {4 + 6 - 7} \right|}}{{\sqrt {1 + 1} }} = \frac{3}{{\sqrt 2 }}\).
Diện tích tam giác \(ABC\) là \({S_{ABC}} = \frac{1}{2}AB.d\left( {C;AB} \right) = \frac{1}{2}.\sqrt 2 .\frac{3}{{\sqrt 2 }} = \frac{3}{2}\).
Khi đó, do \(G\) là trọng tâm tam giác \(ABC\) nên diện tích tam giác \(BCG\) là
\({S_{BCG}} = \frac{1}{3}{S_{ABC}} = \frac{1}{3}.\frac{3}{2} = \frac{1}{2}\).
Câu 4
Lời giải
Đáp án đúng là A
Phương pháp giải
Vận dụng khai triển Newton.
Lời giải
Xét khai triển Newton:
\({(1 + x)^n} = C_n^0{.1^0}.{x^n} + C_n^1{.1^1}.{x^{n - 1}} + \ldots + C_n^n{.1^n}.{x^0} = C_n^0.{x^n} + C_n^1.{x^{n - 1}} + \ldots + C_n^n.{x^0}\) (1)
\(\begin{array}{*{20}{c}}{{{(x + 1)}^n} = C_n^0.{x^0}{{.1}^n} + C_n^1.{x^1}{{.1}^{n - 1}} + \ldots + C_n^n.{x^n}{{.1}^0} = C_n^0.{x^0} + C_n^1.{x^1} + \ldots + C_n^n.{x^n}}\end{array}\)(2)
Cho \(x = 1\), khi đó (1) trở thành \({2^n} = C_n^0 + C_n^1 + \ldots + C_n^n \Leftrightarrow C_n^1 + \ldots + C_n^n = {2^n} - C_n^0 = {2^n} - 1\)
Cho \({2^n} - 1 = 4095 \Leftrightarrow n = 12\).
Nhân theo vế (1) và (2) ta được:
\({(1 + x)^{2n}} = \left( {C_n^0{x^n} + C_n^1{x^{n - 1}} + \ldots + C_n^n{x^0}} \right)\left( {C_n^0{x^0} + C_n^1{x^1} + \ldots + C_n^n{x^n}} \right)\)
Đồng nhất hệ số của \({x^n}\) ta được:
\(C_{2n}^n = {\left( {C_n^0} \right)^2} + {\left( {C_n^1} \right)^2} + \ldots + {\left( {C_n^n} \right)^2} \Leftrightarrow {\left( {C_n^1} \right)^2} + \ldots + {\left( {C_n^n} \right)^2} = C_{2n}^n - 1\)
Cho \(n = 12\), ta được \(S = C_{24}^{12} - 1 = 2704155\).
Lời giải
Đáp án đúng là A
Phương pháp giải
Biến đổi phương trình lượng giác đã cho về dạng các phương trình lượng giác cơ bản.
Lời giải
Biến đổi phương trình đã cho:
\[3{\cos ^2}x - \sin x\cos 2x - \frac{{\sin 2x}}{2} - \cos x\cos 2x + \sin x = 2\]
\( \Leftrightarrow 3{\cos ^2}x - 2 - \sin x\cos 2x - \sin x\cos x - \cos x\cos 2x + \sin x = 0\)
\( \Leftrightarrow 2{\cos ^2}x - 1 + {\cos ^2}x - 1 - \sin x\cos 2x - \sin x\cos x - \cos x\cos 2x + \sin x = 0\)
\( \Leftrightarrow \cos 2x - {\sin ^2}x - \sin x\cos 2x - \sin x\cos x - \cos x\cos 2x + \sin x = 0\)
\( \Leftrightarrow \cos 2x(1 - \sin x - \cos x) + \sin x(1 - \sin x - \cos x) = 0\)
\( \Leftrightarrow (\cos 2x + \sin x)(1 - \sin x - \cos x) = 0\)
\( \Leftrightarrow \left( { - 2{{\sin }^2}x + \sin x + 1} \right)\left( {1 - \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)} \right) = 0\)
\( \Leftrightarrow (\sin x - 1)(2\sin x + 1)\left( {1 - \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin x = 1}\\{\sin x = \frac{{ - 1}}{2}}\\{\sin \left( {x + \frac{\pi }{4}} \right) = \frac{1}{{\sqrt 2 }}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\\{x = \frac{{11\pi }}{6} + k2\pi }\\{x = k2\pi }\\{x = \frac{\pi }{2} + k2\pi }\end{array}(k \in \mathbb{Z})} \right.} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\\{x = \frac{{11\pi }}{6} + k2\pi }\\{x = k2\pi }\end{array}\quad (k \in \mathbb{Z})} \right.\)
Cho \(0 < \frac{\pi }{2} + k2\pi < 2024\pi \Leftrightarrow \frac{{ - 1}}{4} < k < \frac{{4047}}{4} \Rightarrow \) Có 1012 giá trị nguyên của \(k\).
Cho \(0 < \frac{{7\pi }}{6} + k2\pi < 2024\pi \Leftrightarrow \frac{{ - 7}}{{12}} < k < \frac{{12137}}{{12}} \Rightarrow \) Có 1012 giá trị nguyên của \(k\).
Cho \(0 < \frac{{11\pi }}{6} + k2\pi < 2024\pi \Leftrightarrow \frac{{ - 11}}{{12}} < k < \frac{{12133}}{{12}} \Rightarrow \) Có 1012 giá trị nguyên của \(k\).
Cho \(0 < k2\pi < 2024\pi \Leftrightarrow 0 < k < 1012 \Rightarrow \) Có 1011 giá trị nguyên của \(k\).
Khi đó, phương trình đã cho có \(1012 + 1012 + 1012 + 1011 = 4047\) nghiệm trong (\(0;2024\pi \)).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 43
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 45
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
B. khó nói/ nghệ thuật
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 107
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 115
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 117
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
B. Đặc điểm đất, đá.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 127
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
C. Tỉ lệ gia tăng dân số tự nhiên Bun-ga-ri cao hơn Cộng hòa Nam Phi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 151
B. criticize someone strongly
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 152
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 153
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 154
B. No, I prefer staying home.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 155
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 156
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 157
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 158
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 159
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 160
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 161
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 162
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 163
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 164
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 165
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 166
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 167
D. The discipline in his workout routine made him successful and well-equipped for fitness.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 168
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 169
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 170
A. I think there’s a concert happening this weekend. What do you think?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 171
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 172
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 174
B. Sugar
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Biểu đồ cột dưới đây là thông tin điểm thi môn Toán của hai lớp 12 A và 12 B.
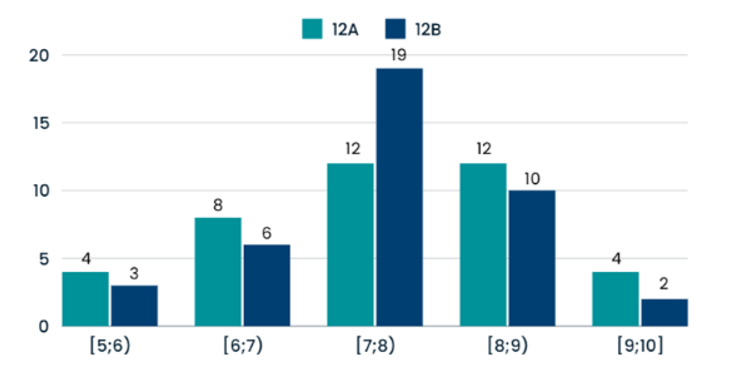
Câu 175
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 176
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 177
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Người Huế luôn quan niệm rằng: “Y phục xứng kỳ đức”. Áo dài Huế được nhiều đối tượng sử dụng, trước nhất là học sinh, sinh viên, viên chức, thanh niên, rồi cả đến những lớp người trung niên, các bà già, chị em làm nghề buôn bán nhỏ ở các cửa hiệu, ở ngoài chợ... Sự khác biệt lớn nhất của áo dài Huế so với các vùng miền khác trong cả nước là được nuôi dưỡng trên nền của một vùng văn hóa từng là Kinh đô cuối cùng của triều đại quân chủ cuối cùng của Việt Nam, nơi mà thẩm mỹ trang phục cung đình nhà Nguyễn với những điển chế nghiêm ngặt đã lan tỏa - giao thoa với thẩm mỹ dân gian để tạo nên những dấu ấn riêng biệt trên chiếc áo dài mà không dễ tìm thấy ở những vùng đất khác. Ngày nay, chiếc áo dài đã trở thành hình ảnh quen thuộc, thân thương, đi vào cuộc sống, gắn liền với nếp văn hóa, tập quán, xuất hiện trong mọi hoạt động lễ nghi, hội hè và cả trong đời thường ở Cố đô Huế. Áo dài còn là nguồn cảm hứng bất tận đi vào thơ, ca, nhạc, họa, trở thành biểu tượng của người phụ nữ Huế. Các hiệu may đo áo dài Huế chủ yếu phân bố tập trung tại các vùng Gia Hội - Chợ Dinh, Kim Long, Vĩ Dạ, Phủ Cam... Đây là những vùng đất có truyền thống lịch sử, văn hóa lâu đời, dân cư tập trung đông đúc và nơi sinh sống của các gia đình, dòng họ có truyền thống may đo áo dài Huế nổi tiếng như: Tân Nghiệp, Minh Tân, Mỹ Lệ, Thẩm, Hùng, Đoan Trang, Phúc, Thảo Trang, Viết Bảo, Quang Hòa, Thanh Châu, Xuân Thi.... Các khâu kỹ thuật cắt, may, luôn tà, làm nút đều được các nghệ nhân, người thợ may áo dài chăm chút thận trọng. Vì vậy, chiếc áo dài không đơn thuần là sản phẩm may mặc mà là cả một tác phẩm nghệ thuật, chứa đựng giá trị bản sắc văn hóa Huế.
(Minh Thông, Tri thức may, mặc áo dài Huế trở thành Di sản văn hóa phi vật thể quốc gia, vov.vn, ngày 13/08/2024)
Câu 178
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 179
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 180
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 181
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 182
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Ai cũng đã từng có lần thấy việc biết một cái tên xác đáng của cái gì trước đó mờ mịt mơ hồ làm cho toàn bộ vấn đề trở nên rõ ràng và minh bạch. Một ý nghĩa nào đấy có vẻ như sắp với đến được bỗng dưng hóa ra không thể tóm bắt nổi; nó khước từ việc cô đúc lại thành hình thái xác định; việc gắn một từ theo cách nào đó (chỉ là thế nào, gần như không thể nói ra được) vạch ra giới hạn của các ý nghĩa, rút nó ra khỏi khoảng trống, đặt cho nó đứng riêng như một thực thể tự thân. Khi Emerson nói rằng ông chẳng thà biết tên gọi thật, tên gọi theo nhà thơ, của một sự vật, còn hơn là biết sự vật đúng thực kia, khi đó ông hẳn đã mang theo trong tâm trí thiên chức soi tỏ và làm sáng rõ của ngôn ngữ này. Niềm vui thích của trẻ nhỏ khi thắc mắc tra hỏi và học tên gọi mọi thứ xung quanh chúng cho thấy ý nghĩa đang trở thành những nhân vật cụ thể đối với chúng, vì thế sự giao dịch của chúng với các sự vật chuyển từ bình diện thể chất sang bình diện trí tuệ. Không có gì đáng ngạc nhiên khi những người hoang dã gắn cho ngôn từ sự linh nghiệm thần bí. Đặt tên cho điều gì tức là ban cho nó một danh hiệu; đề cao và vinh danh nó bằng cách nâng nó từ một sự việc hữu hình lên thành một ý nghĩa rõ ràng và vĩnh viễn. Biết tên gọi của người và sự vật và có thể điều khiển được những cái tên ấy, trong sự thức nhận ban sơ, chính là chiếm lĩnh được phẩm cách và giá trị của chúng, làm chủ chúng.
(John Dewey, Cách ta nghĩ, NXB Tri thức, Hà Nội, 2017)
Câu 183
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 184
B. Nắm được đặc điểm của đối tượng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 185
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 186
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 187
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Những lập luận vững chắc sẽ giúp bạn chứng minh được luận điểm của mình, đồng thời giúp bạn giao tiếp tốt hơn với người khác. Hãy nhớ rằng, tư duy phản biện không xoay quanh việc giành chiến thắng – nó xoay quanh việc theo sát quá trình phát triển luận điểm để đi đến kết luận. Với những kỹ năng tranh biện hiệu quả, bạn sẽ có thể xác định kết luận nào là đúng, cũng như những điểm hợp lý trong luận điểm của người khác. Tranh luận lành mạnh sẽ giúp bạn học hỏi, và từ đó trau chuốt những đức tin và ý tưởng của bạn. Những kỹ năng tranh luận cũng sẽ giúp bạn quen với việc lý luận những ý tưởng của mình, thay vì hợp lý hóa chúng. Hãy nghĩ về hợp lý hóa như là thứ tạo ra thiên kiến xác nhận; đây thường là lúc bạn đưa ra kết luận trước, sau đó mới đưa ra luận điểm để biện hộ cho kết luận đó. Trong khi quá trình lý luận lại hoàn toàn khác. Quá trình lý luận đòi hỏi chúng ta phải thu thập dữ liệu, quan sát và có đủ chứng cứ để đưa ra kết luận. Trùng hợp thay, đây cũng là cách các học giả trong mọi ngành tạo ra công trình học thuật của mình, hoặc ít ra là nên như thế.
(Albert Rutherford, Rèn luyện tư duy phản biện, NXB Phụ nữ, Hà Nội, 2021)
Câu 188
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 190
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 191
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 192
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Trước anh xe tưởng bà khách đi có việc gì, cho nên còn chạy. Sau thấy bà cứ trỏ vơ vẩn hết phố nọ sang phố kia, mà chả đỗ ở phố nào cả, thì mới đoán có lẽ là cánh “ăn sương” chi đây. Anh bèn đi bước một. Nhiều lúc muốn hỏi thực, nếu có phải giăng há thì mình giới thiệu cho một món sộp đáo để. Nhưng lỡ không phải thì họ mắng cho và không trả tiền thì khổ. […]
- Mấy giờ rồi, thưa bà?
- Phải gió nhà nào bây giờ đã đốt pháo giao thừa! Mới có mười hai giờ kém mười lăm.
Anh xe mới nghĩ: “Mười lăm phút nữa, mình sẽ có sáu hào. Sáu hào với hai hào là tám. Thế nào ta cũng nài thêm bà ấy mở hàng cho một hào nữa là chín. Chín hào! Mở hàng ngay từ lúc năm mới vừa đến. Thật là may! Mới năm mới đã phát tài! Thôi, sang năm tất là làm ăn bằng mười bằng trăm năm nay”. Rồi anh nghĩ đến vợ con anh, mà phấn chấn trong lòng, như có cái sức gì nó xúi giục anh quên khổ để vui lòng làm việc vậy. “Sáng mai, kéo chuyến khách qua ga, xong rồi, ta đánh bát phở tái, rồi mua cho con cái bánh ga tô cho nó mừng. Vợ ta nghe thấy trong túi ta có tiền, thì chắc hớn hở, thấy ta làm lụng vất vả để kiếm tiền nuôi cả nhà, tất là thương ta lắm. Nhưng ta sẽ làm ra dáng không mệt nhọc, để vợ chồng con cái ăn tết với nhau cho hể hả”.
Anh vừa nghĩ thế, vừa kéo về phía nhà thương Phủ Doãn. Tới chỗ khi nẫy, anh dừng xe lại, nói:
- Bây giờ có lẽ mười hai giờ, xin bà cho cháu tiền.
Bà khách có ý luống cuống, nói:
- Chết! Anh hỏi tiền tôi bây giờ à? Anh chịu khó kéo tôi một giờ nữa đi.
- Thôi khuya rồi, cháu phải về nhà.
- Này, chả nói giấu gì anh, tôi cũng đi kiếm khách từ tối đến giờ. Có anh biết đấy. Có gặp ai hỏi han gì đâu. Tôi định nếu có khách thì hỏi vay tiền trước để giả anh. Nhưng chẳng may gặp phải cái tối xúi quẩy thế này, thì tôi biết làm thế nào?
- Thế cô đi xe tôi từ chín giờ, cô không giả tiền tôi à?
- Bây giờ thì tôi biết làm thế nào? […]
(Nguyễn Công Hoan, Người ngựa, ngựa người, NXB Văn học, Hà Nội, 2022)
Câu 193
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 194
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 195
B. Giới giang hồ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 196
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 197
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Dải mây trắng đỏ dần trên đỉnh núi,
Sương hồng lam ôm ấp nóc nhà tranh,
Trên con đường viền trắng mép đồi xanh,
Người các ấp tưng bừng ra chợ Tết.
Họ vui vẻ kéo hàng trên cỏ biếc;
Những thằng cu áo đỏ chạy lon xon,
Vài cụ già chống gậy bước lom khom,
Cô yếm thắm che môi cười lặng lẽ.
Thằng em bé nép đầu bên yếm mẹ,
Hai người thôn gánh lợn chạy đi đầu,
Con bò vàng ngộ nghĩnh đuổi theo sau.
(Đoàn Văn Cừ, Chợ Tết, In trong Đoàn Văn Cừ toàn tập, NXB Hội Nhà văn, Hà Nội, 2013)
Câu 198
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 199
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 200
B. So sánh
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 201
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 202
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 7
Tuyến giáp hấp thụ hầu hết iod trong cơ thể. Vì thế iod phóng xạ (I131) thường được dùng điều trị ung thư tuyến giáp. Các tế bào nang giáp bắt giữ iod phóng xạ, bức xạ ion hóa từ iod phóng xạ có thể phá hủy tuyến giáp và những vị trí có tế bào giáp (bao gồm cả tế bào ung thư) có khả năng lưu giữ iod phóng xạ, nhưng ít ảnh hưởng đến các bộ phận khác trong cơ thể. Để điều trị ung thư giáp cần liều iod phóng xạ lớn hơn nhiều so với liều dùng trong phương pháp xạ hình xác định ung thư tuyến giáp.
Phương pháp điều trị này được dùng để hủy mô giáp khi chưa thể phẫu thuật triệt để, hoặc trong các thể ung thư tuyến giáp đã có di căn hạch và di căn tới các cơ quan khác trong cơ thể.
Một bệnh nhân đã nhận một liều dược chất phóng xạ chứa 25mg \(_{53}^{131}I\). Biết rằng \(_{53}^{131}I\) là chất phóng xạ β− và có chu kì bán rã là 8,02 ngày.
Câu 203
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 204
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 205
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 8
Trong hoá học, chuẩn độ là một phương pháp dùng để xác định nồng độ của một chất trong dung dịch bằng một dung dịch khác đã biết nồng độ. Về nguyên tắc, có thể xác định nồng độ của một dung dịch base mạnh bằng một dung dịch acid mạnh (hoặc ngược lại) đã biết trước nồng độ (thường gọi là dung dịch chuẩn) dựa theo phản ứng trung hoà: H+ + OH− → H2O. Những phản ứng giữa các acid mạnh và base mạnh trong dung dịch đều có chung bản chất.
Người ta tiến hành xác định nồng độ của dung dịch NaOH bằng axit oxalic (COOH)2 như sau:
Bước 1: Cân 1,26 gam oxalic acid ngậm nước (H2C2O4.2H2O hoà tan hoàn toàn vào nước, định mức thành 100 mL dung dịch.
Bước 2: Lấy 30 mL dung dịch oxalic acid đã được định mức vào bình tam giác, thêm vài giọt chỉ thị phenolphtalein.
Bước 3: Chuẩn độ dung dịch oxalic acid bằng dung dịch NaOH chưa biết nồng độ đến khi xuất hiện màu hồng (pH = 9) thì hết 23,2 mL dung dịch NaOH.
Câu 206
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 207
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 208
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 9
Hemoglobin là một loại protein có trong hồng cầu, chịu trách nhiệm vận chuyển oxygen trong cơ thể. Hemoglobin cấu tạo gồm bốn chuỗi polypeptide: hai chuỗi α-globin và hai chuỗi β-globin. Mỗi chuỗi polypeptide chứa từ 141 đến 146 amino acid. Bệnh hồng cầu hình lưỡi liềm là một rối loạn di truyền do đột biến gen mã hóa chuỗi β-globin. Dạng đột biến thay thế cặp T-A thành cặp A-T đã biến gene quy định chuỗi β-globin bình thường (HbA) thành gen bị đột biến (HbS), dẫn đến thay đổi amino acid thứ 6 từ glutamic thành valine trong chuỗi polypeptide. Chuỗi β-globin bị đột biến hình thành nên protein hemoglobin S. Khi liên kết với oxygen, hemoglobin S có cấu trúc hình cầu và có tính tan cao. Tuy nhiên, khi giải phóng oxygen, hemoglobin S thay đổi cấu trúc không gian làm chúng có thể kết dính lại với nhau tạo ra những sợi dài (polymer) bên trong hồng cầu làm giảm khả năng mang oxygen và khiến hồng cầu bị biến dạng giống như lưỡi liềm.
Câu 209
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 210
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 211
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 10
Trong thời gian này, Người cũng tập trung cho việc chuẩn bị về tổ chức và cán bộ. Người lập ra Hội Việt Nam cách mạng thanh niên (năm 1925), tổ chức nhiều lớp đào tạo cán bộ tại Quảng Châu (Trung Quốc) và gửi cán bộ đi học tại trường Đại học Phương Đông (ở Liên Xô trước đây) và trường Lục quân Hoàng Phố (Trung Quốc) nhằm đào tạo cán bộ cho cách mạng Việt Nam.
Nhờ hoạt động không mệt mỏi của lãnh tụ Nguyễn Ái Quốc và nhiều đồng chí cách mạng tiền bối mà những điều kiện thành lập Đảng ngày càng chín muồi. Cuối năm 1929, những người cách mạng Việt Nam trong các tổ chức cộng sản đã nhận thức được sự cần thiết và cấp bách phải thành lập một Đảng Cộng sản thống nhất, chấm dứt tình trạng chia rẽ phong trào cộng sản ở Việt Nam. Nguyễn Ái Quốc đã chủ động tổ chức và chủ trì Hội nghị hợp nhất Đảng tại Hong Kong, Trung Quốc từ ngày 3/2 đến ngày 7/2/1930. Hội nghị đã quyết định hợp nhất các tổ chức Đảng (Đông Dương Cộng sản Đảng, An Nam Cộng sản Đảng, Đông Dương Cộng sản Liên đoàn) thành Đảng Cộng sản Việt Nam. Hội nghị thảo luận và thông qua các văn kiện: Chính cương vắn tắt, Sách lược vắn tắt, Chương trình tóm tắt và Điều lệ vắn tắt của Đảng Cộng sản. Những văn kiện đó do Nguyễn Ái Quốc soạn thảo, được Hội nghị hợp nhất Đảng thông qua là sự vận dụng sáng tạo chủ nghĩa Mác – Lê nin vào điều kiện cụ thể của cách mạng Việt Nam. Hội nghị hợp nhất các tổ chức Cộng sản có ý nghĩa như là một Đại hội thành lập Đảng. Những văn kiện được thông qua tại Hội nghị hợp nhất do Nguyễn Ái Quốc chủ trì chính là Cương lĩnh chính trị đầu tiên của Đảng. Ngày 3/2/1930 trở thành ngày thành lập Đảng Cộng sản Việt Nam.
(Theo Viện Hàn lâm khoa học xã hội Việt Nam)
Câu 212
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 213
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 214
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 11
Tháng 2-1990, Tổng thống Cộng hòa Nam Phi- Đơ Clec tuyên bố từ bỏ chính sách Apacthai, đồng thời các Đảng phái chính trị ở Nam Phi như: Đại hộc dân tộc Phi (ANC), Đại hội toàn châu Phi (PAC) được hoạt động hợp pháp. Chủ tịch ANC, ông Nenxon Manđêla được tự do sau 27 năm cầm tù.
Tháng 11-1993, sau 3 năm đàm phán, 21 đảng phái ở Nam Phi đã thông qua Hiến pháp mới, chấm dứt sự tồn tại trên ba thế kỉ của chế độ Apacthai ở Nam Phi. Sau cuộc bầu cử đa chủng tộc đầu tiên ở Nam Phi (4-1994), ngày 10-5-1994, chủ tịch ANC Nenxon Manđêla tuyên thệ nhậm chức Tổng thống và trở thành Tổng thống da đen đầu tiên trong lịch sử tồn tại của đất nước này, trước sự vui mừng của hàng triệu người dân Nam Phi và hàng nghìn quan khách từ khắp nơi trên thế giới. Công hòa Nam Phi bước sang một thời kì phát triển mới.
(Lịch sử thế giới hiện đại trang 388)
Câu 215
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 216
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 217
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 12
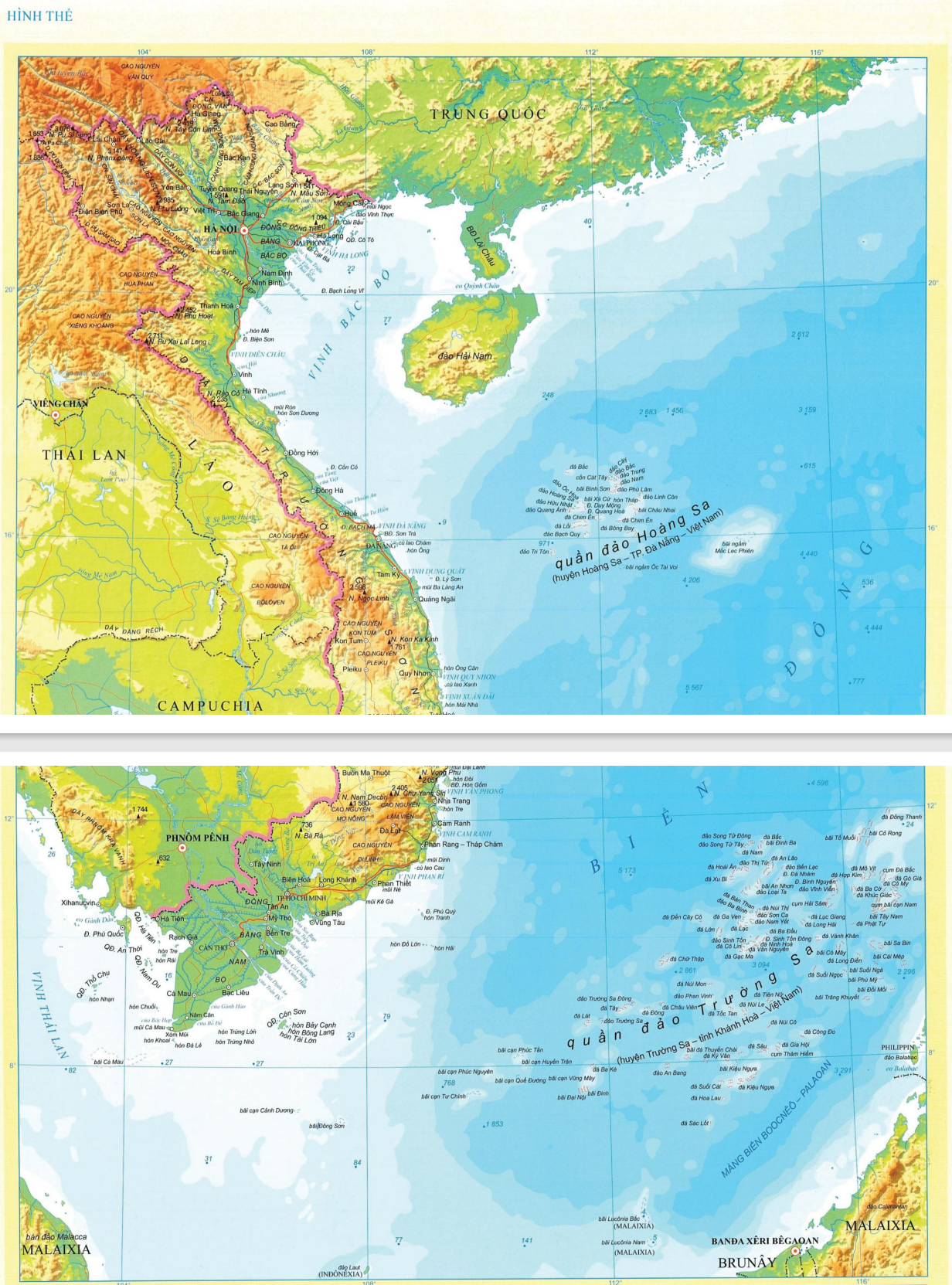
(Atlat Địa lí Việt Nam, Nxb Giáo dục Việt Nam, 2024)
Câu 218
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 219
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 220
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 13
Schools in the United States have not always had a large number of libraries. As recently as 1958 about half of the public schools in the United States had no libraries at all. The number of public school libraries increased dramatically when the federal government passed the Elementary and Secondary Education Act of 1965, which provided funds for school districts to improve their education programs and facilities, (631) __________ their libraries. Nevertheless, many educators claim that since the legislation was passed federal spending has not increased (632) _____________ to meet the rising cost of new library technologies such as computer databases and Internet access.
(633) ______________, individual school districts rely on funds from local property taxes to meet the vast majority of public schools expenses. Therefore, the libraries of public schools tend to reflect the financial capabilities of the communities (634) ______________. Districts in wealthy suburbs often have fully staffed libraries for abundant resources, spacious facilities, and curricular and instructional support. In contrast, school districts in many poor areas house their libraries in ordinary classrooms or in small rooms. The libraries in such areas are generally staffed by volunteers, who organize and maintain books that are often out-of-date, (635) ____________, or damaged.
Câu 221
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 222
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 223
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 224
D. are located in
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 225
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 14
The increase in international business and in foreign investment has created a need for executives with knowledge of foreign language and skills in cross-cultural communication. Americans, however, have not been well trained in either area and, consequently, have not enjoyed the same level in negotiation in an international arena as have their foreign counterparts.
Negotiating is the process of communicating back and forth for the purpose of reaching an agreement. Involves persuasion and compromise, but in order to participate in either one, the negotiators must understand the ways in which people are persuaded and how compromise is reached within the culture of negotiation.
In many international negotiations business abroad, Americans are perceived as wealthy and impersonal. It often appears to the foreign negotiator that Americans represents a large multimillion–dollar corporation that can afford to pay the price without bargaining further. The American negotiator’s role became that of and impersonal purveyor of information and cash, the image that succeeds only in underming the negotiation.
In studies of American negotiators abroad, several traits have been identified that may serve to confirm that stereotypical perception, while subverting the negotiator’s position. Two traits in particular that cause cross-cultural misunderstanding are directness and impatience on that part of Amarican negotiator. Furthermore, American negotiators often insist on realizing short-term goals. Foreign negotiators, on the other hand, may value the relationship established between negotiators and may be willing to invest time in it for long-term benefits. In order to solidify the relationship, they may opt for indirect interactions without regard for the time involved in getting to know the other negotiator.
Clearly, perceptions and differences in values affect the outcomes of negotiation and the success of negotiators. For Americans to play a more effective role in international business negotiations, they must put forth more effort to improve cross-cultural understanding.
Câu 226
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 227
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 228
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 229
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 230
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 15
Picture a society where learning can happen any time, in any place and can be completed without ever going to class. This could be the new wave of education and the Internet technology now exists to support such a system. The virtual classroom is here. If you are interested in English, or Civil Engineering, then head to the university and click yourself a degree. Well, maybe it’s not that easy, but you would be on the right track. The flexibility of studying at your own pace, and the money you save with online courses are two of the main attractions.
The Web is a powerful education tool. Yet some feel that virtual classrooms will isolate students from each other, which will result in problems developing interpersonal relationships and that these skills are much more important than computer skills. Should teachers teach kids how to behave in society, how to respect others and how to cooperate or should kids have already learned this from their parents? No one is saying that social skills aren’t important; however, virtual classrooms are far about more than just computer skills. Some strongly believe that education can be taught via the Web and social skills can be gained from joining sports team, summer camps or just hanging out! Others argue that this virtual classroom may place pressure on students; to become computer literate or be left behind in life. Is this undue pressure or reality? Maybe being left behind in life is a little dramatic but the reality is that the computer age is here. Whether you want to pay for your new jeans with your debit cards, or check to see if the library has the book you want, you’re going to need some computer skills.
The development of flexible, inquiring minds has rarely been the main concern in the design of educational systems. After all, if you have over thirty inquiring minds and only one teacher, flexibility could be a problem. It seems that developing students’ proper social behavior has always exceeded the concern of the students’ creativity. Computer technology can make individualized attention a real possibility. At the Institute for the Learning Sciences, systems are being developed to allow people to try out things in simulated worlds. This technology will allow for the individual creative growth in students.
The Web will provide amazing opportunities for the education of our society. Anyone with a phone line and a computer has access to unlimited amounts of knowledge and programs designed to help them learn and understand. The teachers and parents involved with these programs will be given the job making interaction with their friends and neighbors. Imagine your recreation room has now become your classroom, and your parents seem to be doing as much homework as you are! So, be prepared as the virtual classroom may find its way to a computer screen near you.
Câu 231
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 232
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 233
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 234
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 235
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.