(1,5 điểm) Tháp Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày mặt trời tạo với mặt đất một góc xấp xỉ \(68^\circ \) và bóng của tòa nhà trên mặt đất dài khoảng \(79{\rm{ m}}{\rm{.}}\)
a) Viết tỉ số lượng giác sin và tan của góc \[ACB\] theo \(AB,\,\,BC,\,\,CA.\)
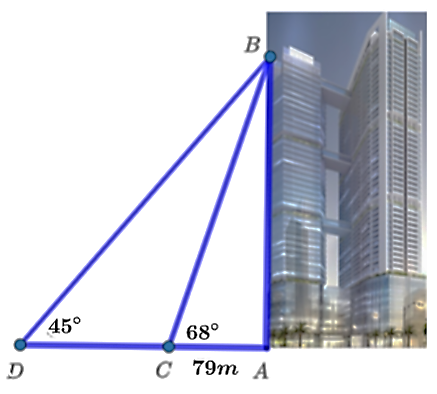
(1,5 điểm) Tháp Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày mặt trời tạo với mặt đất một góc xấp xỉ \(68^\circ \) và bóng của tòa nhà trên mặt đất dài khoảng \(79{\rm{ m}}{\rm{.}}\)
a) Viết tỉ số lượng giác sin và tan của góc \[ACB\] theo \(AB,\,\,BC,\,\,CA.\)
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \[\tan \widehat {ACB} = \frac{{AB}}{{BC}}\] và \[\tan \widehat {ACB} = \frac{{AB}}{{AC}}.\]
Câu hỏi cùng đoạn
Câu 2:
b) Một người đang đi về phía tòa nhà với phương nhìn lên đỉnh tạo với phương nằm ngang một góc bằng \(45^\circ \). Biết người đó mất 140 giây để đi đến tòa nhà. Tính vận tốc trung bình của người đó (làm tròn kết quả đến chữ số thập phân thứ nhất).
Giải bởi Vietjack
b) Chiều cao của tòa tháp chính là độ dài đoạn \(AB\).
Ta có: \[AB = AC \cdot \tan \widehat {ACB} = 79 \cdot \tan 68^\circ {\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Xét tam giác \(ABD\) vuông tại \(A\), ta có: \(AB = BD \cdot \sin \widehat {ADB}\)
Suy ra \(BD = \frac{{AB}}{{\sin \widehat {ADB}}} = \frac{{79 \cdot \tan 68^\circ }}{{\sin 45^\circ }} \approx 276,52{\rm{ (m)}}{\rm{.}}\)
Vận tốc trung bình của chiếc người đó khoảng: \(276,52:140 \approx 2,0{\rm{ (m/s)}}{\rm{.}}\)
Vậy vận tốc trung bình của người đó là khoảng \(2{\rm{ m/s}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Điều kiện xác định \(x \ne - 1,\,\,x \ne 1.\)
Ta có: \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{4}{{1 - {x^2}}}\)
\[\frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{ - 4}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\]
\(\frac{{{{\left( {x - 1} \right)}^2} - {{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{ - 4}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\({\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = - 4\)
\(\left( {x - 1 + x + 1} \right)\left( {x - 1 - x - 1} \right) = - 4\)
\(2x.\left( { - 2} \right) = - 4\)
\( - 4x = - 4\)
\(x = 1\) (không thỏa mãn).
Vậy phương trình đã cho vô nghiệm.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
![a) Chứng minh bốn điểm \[A,M,O,N\] cùng thuộc một đường tròn. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/2-1766542632.png)
a) Vì \(AM,\,\,AN\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) lần lượt tại \(M,\,\,N\) nên \(AM \bot OM,\,\,AN \bot ON.\)
Gọi \[E\] là trung điểm của \[OA\]. Khi đó \(OE = AE = \frac{1}{2}OA.\)
Xét \[\Delta MOA\] vuông tại \[M\] có \[ME\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[ME = \frac{1}{2}OA\].
Xét \[\Delta NOA\] vuông tại \[N\] có \[NE\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[NE = \frac{1}{2}OA\].
Vì \[NE = ME = OE = AE = \frac{1}{2}OA\] nên bốn điểm \[A,M,O,N\] cùng thuộc đường tròn tâm \[E,\] đường kính \[OA\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập