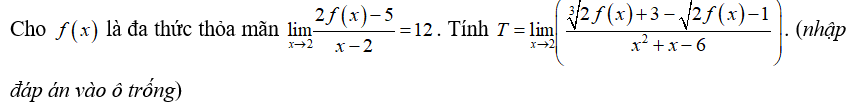Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là "-2/5"
Phương pháp giải
Đặt \(g\left( x \right) = \frac{{2f\left( x \right) - 5}}{{x - 2}}\), biến đổi xác định giới hạn của hàm số \(f\left( x \right)\) khi \(x\) tiến đến 2
Lời giải
Đặt \(g\left( x \right) = \frac{{2f\left( x \right) - 5}}{{x - 2}}\)
\( \Rightarrow \left( {x - 2} \right).g\left( x \right) = 2f\left( x \right) - 5 \Rightarrow f\left( x \right) = \frac{{\left( {x - 2} \right)g\left( x \right)}}{2} + \frac{5}{2}\)
Ta có:
\( = \mathop {\lim }\limits_{x \to 2} \left( {\frac{{\sqrt[3]{{2f(x) + 3}} - 2}}{{(x - 2)(x + 3)}} - \frac{{\sqrt {2f(x) - 1} - 2}}{{(x - 2)(x + 3)}}} \right)\)
\( = \mathop {\lim }\limits_{x \to 2} \left( {\frac{{2f(x) - 5}}{{(x - 2)(x + 3).\left( {\sqrt[3]{{{{(2f(x) + 3)}^2}}} + 2\sqrt[3]{{2f(x) + 3}} + 4} \right)}} - \frac{{2f(x) - 5}}{{(x - 2)(x + 3)(\sqrt {2f(x) - 1} + 2)}}} \right)\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{2f(x) - 5}}{{x - 2}}.\left( {\frac{1}{{(x + 3)\left( {\sqrt[3]{{{{(2f(x) + 3)}^2}}} + 2\sqrt[3]{{2f(x) + 3}} + 4} \right)}} - \frac{1}{{(x + 3).(\sqrt {2f(x) - 1} + 2)}}} \right)\)
\( = 12.\left( {\frac{1}{{60}} - \frac{1}{{20}}} \right) = \frac{{ - 2}}{5}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "1/4 | 0,25"
Phương pháp giải
Vận dụng công thức: \(E = \frac{F}{{|q|}}\)
Định luật Coulomb: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Lời giải
Theo định luật Coulomb ta có: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
mặt khác: \(E = \frac{F}{{|q|}}\)
\( \Rightarrow E = k\frac{{|Q|}}{{\varepsilon .{r^2}}}\)
Giả sử môi ô vuông là 1 đơn vị đo.
Ta có:
\( \Rightarrow {E_1} = k\frac{{|Q|}}{{{\varepsilon _1}.r_1^2}}\)
\( \Rightarrow {E_2} = k\frac{{|Q|}}{{{\varepsilon _2}.r_2^2}}\)
Xét tại điểm \({E_1} = {E_2}\) ứng với \[{r_1} = {r_2}\]
\( \Rightarrow k\frac{{|Q|}}{{{\varepsilon _1}.r_1^2}} = k\frac{{|Q|}}{{{\varepsilon _2}.r_2^2}}\)
\( \Leftrightarrow \frac{1}{{{\varepsilon _1}r_1^2}} = \frac{1}{{{\varepsilon _2}r_2^2}} \Rightarrow \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \frac{{r_2^2}}{{r_1^2}} = 0,25\)
Lời giải
Đáp án đúng là "69/2"
Phương pháp giải
Lập hàm và dùng ứng dụng hàm số để giải bài toán
Lời giải
Gọi giá bán mới là \(x\) triệu đồng với \(x \in \left[ {30;35} \right]\)
Khi đó số xe bán ra là \(400 + \left( {35 - x} \right)100\).
Lợi nhuận thu được là:
\(f\left( x \right) = \left[ {400 + \left( {35 - x} \right)100} \right]\left( {x - 30} \right) = - 100{x^2} + 6900x - 117000 = - 100{\left( {x - \frac{{69}}{2}} \right)^2} + 2025 \le 2025\)
Dấu bằng xảy ra khi \(x = \frac{{69}}{2}\). Vậy giá bán mới \(\frac{{69}}{2}\) triệu đồng thì thu được lợi nhuận cao nhất.
Câu 3
A. \(106{\rm{d}}{{\rm{m}}^3}\).
B. \(106\;{{\rm{m}}^3}\).
C. \(106\;{\rm{c}}{{\rm{m}}^3}\).
D. \(106\;{\rm{m}}{{\rm{m}}^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Hà Nội có biên độ nhiệt nhỏ hơn Cà Mau do ảnh hưởng của gió mùa Đông Bắc vào mùa đông.
B. Cà Mau có mùa khô sâu sắc hơn Hà Nội do ảnh hưởng của gió mùa Tây Nam vào mùa hạ.
C. Hà Nội có một số tháng nhiệt độ dưới 20℃ là do ảnh hưởng của gió Tín phong bán cầu Bắc.
D. Hà Nội có mùa khô ít sâu sắc hơn là do ảnh hưởng của gió mùa Đông Bắc vào cuối mùa đông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Phần lớn dân số nước ta sinh sống ở thành thị.
B. Tỉ lệ dân nông thôn thấp hơn dân thành thị.
C. Tỉ lệ dân thành thị năm 2020 rất cao.
D. Số dân thành thị giai đoạn 2000 – 2015 tăng nhanh nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập