Cho hình chóp \[S.ABCD{\rm{ c\'o }}SA \bot \left( {{\rm{ }}ABCD} \right),\] đáy \[ABCD\] là hình chữ nhật. Biết \[AD = 2a,\] \[SA = a.\] Khoảng cách từ \[A\] đến \[\left( {SCD} \right)\] bằng
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 11 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
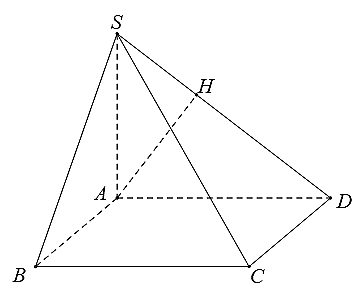
Ta có \[SA \bot \left( {ABCD} \right)\] nên \[SA \bot CD\].
Vì \[ABCD\] là hình chữ nhật nên \[AD \bot CD\].
Suy ra \[\left( {SAD} \right) \bot CD\].
Trong \[\left( {SAD} \right)\] kẻ \[AH\] vuông góc \[SD\] tại \[H\].
Khi đó ta chứng minh được \[AH \bot \left( {SCD} \right)\].
Suy ra \[d\left( {A,\left( {SCD} \right)} \right) = AH = \] \(\frac{{SA \cdot AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{a \cdot 2a}}{{\sqrt {{a^2} + {{\left( {2a} \right)}^2}} }} = \frac{{2a}}{{\sqrt 5 }}.\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: C
Vì \(SA \bot \left( {ABC} \right)\) nên \[SA \bot BC\]. Lại có \(BC \bot AB\) (do tam giác \(ABC\) là tam giác vuông tại \(B\)). Từ đó suy ra \(BC \bot \left( {SAB} \right)\), do đó \(BC \bot SB\).
Ta có \(\left( {SBC} \right) \cap \left( {ABC} \right) = BC\), \(AB \bot BC,\,\,SB \bot BC\)
\( \Rightarrow \widehat {SBA}\) là một góc phẳng của góc nhị diện \(\left[ {A,BC,S} \right]\).
Ta có \(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \sqrt 3 \Rightarrow \widehat {SBA} = 60^\circ \).
Vậy số đo của góc nhị diện \(\left[ {A,BC,S} \right]\) bằng \(60^\circ .\)
Câu 2
Lời giải
Đáp án đúng là: D
\[P = \frac{{{a^{\sqrt 3 + 1}} \cdot {a^{2 - \sqrt 3 }}}}{{{{\left( {{a^{\sqrt 2 - 2}}} \right)}^{\sqrt 2 + 2}}}} = \frac{{{a^{\sqrt 3 + 1 + 2 - \sqrt 3 }}}}{{{a^{\left( {\sqrt 2 - 2} \right)\left( {\sqrt 2 + 2} \right)}}}} = \frac{{{a^3}}}{{{a^{ - 2}}}} = {a^5}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập