a) Tìm tất cả các số thực a sao cho \(a + \sqrt {2023} \) và \(\frac{{999}}{a} + \sqrt {2023} \) đều là các số nguyên.
b) Cho hai số thực dương \(a,b\) thỏa mãn \(4{a^2} + {b^2} = 2\). Tìm giá trị nhỏ nhất của biểu thức
\(T = \frac{{4a}}{{2 + b}} + \frac{b}{{1 + a}} + \frac{{2024}}{{2a + b}}\).
a) Tìm tất cả các số thực a sao cho \(a + \sqrt {2023} \) và \(\frac{{999}}{a} + \sqrt {2023} \) đều là các số nguyên.
b) Cho hai số thực dương \(a,b\) thỏa mãn \(4{a^2} + {b^2} = 2\). Tìm giá trị nhỏ nhất của biểu thức
\(T = \frac{{4a}}{{2 + b}} + \frac{b}{{1 + a}} + \frac{{2024}}{{2a + b}}\).Quảng cáo
Trả lời:
a) Tìm tất cả các số thực a sao cho \(a + \sqrt {2023} \) và \(\frac{{999}}{a} + \sqrt {2023} \) đều là các số nguyên.
Đặt \[\left\{ \begin{array}{l}x = a + \sqrt {2023} \\y = \frac{{999}}{a} + \sqrt {2023} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = x - \sqrt {2023} \\y = \frac{{999}}{{x - \sqrt {2023} }} + \sqrt {2023} \end{array} \right..\]
Ta có \[y = \frac{{999}}{{x - \sqrt {2023} }} + \sqrt {2023} \Leftrightarrow xy - y\sqrt {2023} = 999 + x\sqrt {2023} - 2023\]
\[ \Leftrightarrow xy + 1024 = \left( {x + y} \right)\sqrt {2023} \].
Vì x, y nguyên nên \(x + y = 0\), suy ra \(y = - x\) và \(xy + 1024 = 0\).
Do đó \(x = \pm 32\). Vậy \(a = \pm 32 - \sqrt {2023} \).
b) Cho hai số thực dương \(a,b\) thỏa mãn \(4{a^2} + {b^2} = 2\). Tìm giá trị nhỏ nhất của biểu thức
\(T = \frac{{4a}}{{2 + b}} + \frac{b}{{1 + a}} + \frac{{2024}}{{2a + b}}\).
Ta có \[4{a^2} + {b^2} \ge 4ab \Leftrightarrow 2\left( {4{a^2} + {b^2}} \right) \ge {\left( {2a + b} \right)^2}\]
\( \Leftrightarrow 4 \ge {\left( {2a + b} \right)^2} \Leftrightarrow 2a + b \le 2 \Leftrightarrow a + \frac{b}{2} \le 1\).
Đặt \(x = a;y = \frac{b}{2}\) , ta có \(x + y \le 1\).
Khi đó \(\frac{1}{2}T = \frac{a}{{1 + \frac{b}{2}}} + \frac{b}{{2\left( {1 + a} \right)}} + \frac{{506}}{{a + \frac{b}{2}}} = \frac{x}{{1 + y}} + \frac{y}{{1 + x}} + \frac{{506}}{{x + y}}.\)
Áp dụng bất đẳng thức Cauchy, ta có
• \(\frac{x}{{1 + y}} + \frac{4}{9}x\left( {1 + y} \right) \ge \frac{4}{3}x \Leftrightarrow \frac{x}{{1 + y}} \ge \frac{8}{9}x - \frac{4}{9}xy\).
• \(\frac{y}{{1 + x}} + \frac{4}{9}y\left( {1 + x} \right) \ge \frac{4}{3}y \Leftrightarrow \frac{y}{{1 + x}} \ge \frac{8}{9}y - \frac{4}{9}xy\).
Suy ra \(\frac{1}{2}T \ge \frac{8}{9}\left( {x + y} \right) - \frac{8}{9}xy + \frac{{506}}{{x + y}} \ge \frac{8}{9}\left( {x + y} \right) + \frac{8}{{9(x + y)}} + \frac{{4546}}{{9(x + y)}} - \frac{8}{9}xy\).\( \ge \frac{8}{9}.2 + \frac{{4546}}{9} - \frac{8}{9}.\frac{1}{4} = \frac{{1520}}{3}\). ( để ý \(xy \le {\left( {\frac{{x + y}}{2}} \right)^2} \le \frac{1}{4}\))
Do đó \(T \ge \frac{{3040}}{3}\). Dấu “\( = \)” xảy ra khi và chỉ khi \(x = y = \frac{1}{2}\) hay \(a = \frac{1}{2};b = 1\).
Vậy giá trị nhỏ nhất của T bằng \(\frac{{3040}}{3}\) đạt được khi \(a = \frac{1}{2};b = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
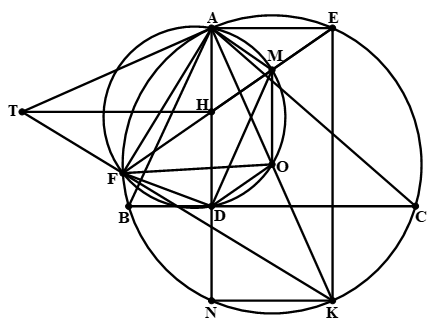
a) Chứng minh M là trung điểm của EH và AMOF là tứ giác nội tiếp.
Vì hai dây AE và BC song song nên AH vuông góc với AE và trung trực của BC cũng là trung trực của AE.
Tam giác AEH vuông tại A nên đường trung trực của AE cũng chính là đường trung bình của tam giác đó. Suy ra M là trung điểm của EH.
Do đó \(MA = ME = MH\), suy ra \(\widehat {AMH} = \widehat {AEM} + \widehat {EAM} = 2\widehat {AEM}\), hay \(\widehat {AMF} = 2\widehat {AEF}\).
Mặt khác, ta có \(\widehat {AOF} = 2\widehat {AEF}\) (góc ở tâm và góc nội tiếp cùng chắn chung AF)
Suy ra \(\widehat {AMF} = \widehat {AOF}\), do đó tứ giác AMOF nội tiếp. (1)
b) Chứng minh \(\widehat {OFA} + \widehat {ODF} = 180^\circ .\)
Gọi N là giao điểm thứ hai của AH với (O).
Ta có \(\widehat {CBN} = \widehat {CAN}\) (cùng chắn cung CN).
Ta lại có \(\widehat {CBH} = \widehat {CAN}\) (cùng phụ với \(\widehat {ACB}\)). Suy ra \(\widehat {CBH} = \widehat {CBN}\).
Tam giác BHN có BD vừa là đường cao vừa là phân giác nên D là trung điểm của HN.
Tứ giác AENF nội tiếp (O) và AN cắt EF tại H nên ta có
\({\rm{HA}}{\rm{.HN = HE}}{\rm{.HF}} \Leftrightarrow HA.2HD = 2HM.HF \Leftrightarrow HA.HD = HM.HF\).
Suy ra tứ giác AMDF nội tiếp. (2)
Từ (1) và (2) ta có AODF nội tiếp. Suy ra \[\widehat {OAF} + \widehat {ODF} = 180^\circ \].
Mặt khác, tam giác OAF cân tại O nên \(\widehat {OAF} = \widehat {OFA}\).
Suy ra \[\widehat {OFA} + \widehat {ODF} = 180^\circ \].
c) Gọi K là điểm đối xứng với A qua O. Tiếp tuyến của (O) tại A cắt đường thẳng FK tại T. Chứng minh hai đường thẳng TH và BC song song với nhau.
Ta có \(\widehat {ATF} = \widehat {FAK}\) (cùng phụ với \(\widehat {AKF}\)). (3)
Ta lại có \(\widehat {EAN} = 90^\circ \) nên EN là đường kính của (O).
Tứ giác AEKN có hai đường chéo AK và NE bằng nhau và cắt nhau tại trung điểm mỗi đường nên AEKN là hình chữ nhật. Suy ra \(AE = NK\), hay
Ta có
Từ (3) và (4) suy ra \(\widehat {ATF} = \widehat {AHE}\), do đó tứ giác ATFH là tứ giác nội tiếp.
Suy ra \(\widehat {AHT} = \widehat {AFT} = 90^\circ \).
Ta có \(AH \bot TH\) và \(AH \bot BC\) nên \(TH{\rm{ // }}BC\).
Lời giải
a) Tìm m để phương trình \({x^2} - 2\left( {m - 1} \right)x - {m^2} + 2m - 3 = 0\) (x là ẩn số) có hai nghiệm\({x_1},{\rm{ }}{x_2}\) thỏa mãn \(\sqrt {x_1^2 + 1} - {x_1} = \sqrt {x_2^2 + 1} + {x_2}\).
Ta có \(ac = - {\left( {m - 1} \right)^2} - 2 < 0\), với mọi m.
Suy ra phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có \(\sqrt {x_1^2 + 1} - {x_1} = \sqrt {x_2^2 + 1} + {x_2} \Leftrightarrow \sqrt {x_1^2 + 1} - \sqrt {x_2^2 + 1} = {x_1} + {x_2}\)
\( \Leftrightarrow \frac{{x_1^2 - x_2^2}}{{\sqrt {x_1^2 + 1} + \sqrt {x_2^2 + 1} }} = {x_1} + {x_2} \Leftrightarrow \frac{{\left( {x_1^{} - x_2^{}} \right)\left( {{x_1} + {x_2}} \right)}}{{\sqrt {x_1^2 + 1} + \sqrt {x_2^2 + 1} }} = {x_1} + {x_2}\)
\( \Leftrightarrow \left[ \begin{array}{l}{x_1} + {x_2} = 0\\\sqrt {x_1^2 + 1} + \sqrt {x_2^2 + 1} = {x_1} - {x_2}\end{array} \right..\)
TH1: \({x_1} + {x_2} = 0 \Leftrightarrow 2(m - 1) = 0 \Leftrightarrow m = 1\).
TH2: \(\sqrt {x_1^2 + 1} + \sqrt {x_2^2 + 1} = {x_1} - {x_2} \Leftrightarrow \left( {\sqrt {x_1^2 + 1} - {x_1}} \right) + \left( {\sqrt {x_2^2 + 1} + {x_2}} \right) = 0\) (vô lý).
Vậy \(m = 1\).
b) Giải phương trình \(2\left( {\sqrt {x + 9} - 3} \right)\left( {\sqrt {9 - x} + 3} \right) = 9.\)
Điều kiện: \( - 9 \le x \le 9\).
Ta có \(\left( {\sqrt {x + 9} - 3} \right)\left( {\sqrt {9 - x} + 3} \right) = \frac{9}{2} \Leftrightarrow \sqrt {81 - {x^2}} + 3\left( {\sqrt {x + 9} - \sqrt {9 - x} } \right) - \frac{{27}}{2} = 0.\)
Đặt \(t = \sqrt {x + 9} - \sqrt {9 - x} \), suy ra \({t^2} = 18 - 2\sqrt {81 - {x^2}} \), ta có phương trình
\(\frac{{18 - {t^2}}}{2} + 3t - \frac{{27}}{2} = 0 \Leftrightarrow - \frac{{{t^2}}}{2} + 3t - \frac{9}{2} = 0 \Leftrightarrow - \frac{1}{2}{(t - 3)^2} = 0 \Leftrightarrow t = 3\).
Với \(t = 3\), ta có \(\sqrt {x + 9} - \sqrt {9 - x} = 3 \Leftrightarrow \sqrt {x + 9} = 3 + \sqrt {9 - x} \)
\( \Leftrightarrow x + 9 = 18 - x + 6\sqrt {9 - x} \Leftrightarrow 6\sqrt {9 - x} = 2x - 9\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{9}{2}\\36(9 - x) = 4{x^2} - 36x + 81\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{9}{2}\\4{x^2} = 243\end{array} \right. \Leftrightarrow x = \frac{{9\sqrt 3 }}{2}\) (thỏa mãn).
Vậy \(S = \left\{ {\frac{{9\sqrt 3 }}{2}} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.