Tìm tất cả các giá trị của m để phương trình \({x^2} - 5x + 3m + 1 = 0\) (x là ẩn, m là tham số) có hai nghiệm phân biệt \({x_1},\;{x_2}\) thỏa mãn \(\left| {x_1^2 - x_2^2} \right| = 15\).

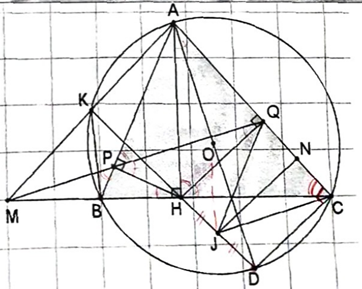
a) Tứ giác APHQ có

\(\widehat {APH} = {90^0}\) (gt)

\(\widehat {AQH} = {90^0}\)   (gt)

=> \(\widehat {APH} + \widehat {AQH} = {180^0}\) và hai góc này ở vị trí đối nhau nên APHQ là tứ giác nội tiếp được đường tròn

=> \(\widehat {PQH} = \widehat {BAH}\)

b) Xét và có

\(\widehat {PQH} = \widehat {BHA}\) (cmt), mà \(\widehat {BAH} = \widehat {BHP}\) (cùng phụ \(\widehat {PBH})\) suy ra \(\widehat {MQH} = \widehat {MHP}\)

\(\widehat {PMH}\) là góc chung

Chứng minh được tứ giác BPQC là tứ giác nội tiếp \( \Rightarrow \widehat {MBP} = \widehat {MQC}\) (cùng bù \(\widehat {PBC}\))

Ta lại có \(\widehat {BMP}\) là góc chung

 (g.g) \( \Rightarrow \frac{{MB}}{{MQ}} = \frac{{MP}}{{MC}}\; \Leftrightarrow M{H^2} = MP.MQ\)   (1)

 (g.g) \( \Rightarrow \frac{{MQ}}{{MH}} = \frac{{MH}}{{MP}} \Leftrightarrow M{H^2} = MP.MQ\)      (2)

Từ (1) và (2) \( \Rightarrow M{H^2} = MB.MC.\)

c) Vì AKBC là tứ giác nội tiếp nên \(\widehat {MKB} = \widehat {MCA}\) (cùng bù với \(\widehat {AKB}\)), mà \(\widehat {AMC}\) là góc chung

Mà \(M{H^2} = MB.MC \Rightarrow M{H^2} = MB.MC \Rightarrow M{H^2} = MK.MA.\)

Do vuông tại H \( \Rightarrow HK\) là đường cao của tam giác AHM (vì

\( \Rightarrow AK \bot KH \Rightarrow AK \bot KD\) suy ra AD là đường kính của (O).

Suy ra \(\widehat {ACD} = {90^0}\) nên \(DC \bot AC\)

Mà \(HQ \bot AC \Rightarrow DC//HQ\) nên HQCD là hình thang.

Gọi N là trung điểm của QC (3) \( \Rightarrow JN\) là đường trung bình của hình thang HQCD

\( \Rightarrow JN//HQ \Rightarrow JN \bot QC\) (4)

Từ (3) và (4) \( \Rightarrow JN\) là đường trung trực của \(QC \Rightarrow JQ = JC\)

a) Ta có \({x^2} + x + 6 = {n^2};\left( {n,\;x \in \mathbb{Z}} \right) \Rightarrow 4{x^2} + 4x + 24 = 4{n^2}\)

     \( \Leftrightarrow 4{x^2} + 4x + 1 - 4{n^2} = - 23 \Leftrightarrow \left( {2x + 1 - 2n} \right)\left( {2x + 1 + 2n} \right) = - 23\)

TH1: \(\left\{ {\begin{array}{*{20}{c}}{2x + 1 - 2n = 1}\\{2x + 1 + 2n = 3}\end{array} \Rightarrow x = 5} \right.\)

TH2: \(\left\{ {\begin{array}{*{20}{c}}{2x + 1 - 2n = 1\;\;\;}\\{2x + 1 + 2n = - 23}\end{array} \Rightarrow x = - 6} \right.\)

b) Tìm nghiệm nguyên của phương trình \({y^2} = - 2\left( {{x^6} - {x^3}y - 32} \right).\)

Ta có \({y^2} = - 2({x^6} - {x^3}y - 32 \Leftrightarrow {x^6} + {\left( {y - {x^3}} \right)^2} = 64\)

\( \Rightarrow {x^6} \le 64 \Leftrightarrow x \le 2\) do \(x \in \mathbb{Z} \Rightarrow x \in \left\{ { - 1; - 2;0;1;2} \right\}\)

Xét các trường hợp:

+ \(x = 2 \Rightarrow {\left( {y - {x^3}} \right)^2} = 0 \Rightarrow y = 8\)

+ \(x = 1 \Rightarrow {\left( {y - {x^3}} \right)^2} = 63 \Rightarrow y \notin \mathbb{Z}\)   (loại)

+ \(x = 0 \Rightarrow {\left( {y - {x^3}} \right)^2} = 64 \Rightarrow y = 8\) và \(y = - 8\)

+ \(x = - 1 \Rightarrow {\left( {y - {x^3}} \right)^2} = 63 \Rightarrow y \notin \mathbb{Z}\) (loại)

+\(x = - 2 \Rightarrow {\left( {y - {x^3}} \right)^2} = 0 \Rightarrow y = - 8\)

Vậy nghiệm của phương trình là: \(\left( {0;8} \right);\left( {0; - 8} \right);\left( {2;8} \right);\left( { - 2; - 8} \right)\).