Cho hai hàm số \(y = f\left( x \right) = {x^2}\) và \(y = g\left( x \right) = 3ax - {a^2}\) với \(a \ne 0\) là tham số.
a. Vẽ đồ thị hàm số \[y = f\left( x \right)\] trên hệ trục tọa độ \[{\rm{Oxy}}\].
b. Chứng minh rằng đồ thị hàm số đã cho luôn có hai giao điểm.
c. Gọi \[{{\rm{y}}_1};{y_2}\]là tung độ giao điểm của hai đồ thị. Tìm \[a\]để \[{{\rm{y}}_1} + {y_2} = 28\].
Cho hai hàm số \(y = f\left( x \right) = {x^2}\) và \(y = g\left( x \right) = 3ax - {a^2}\) với \(a \ne 0\) là tham số.
a. Vẽ đồ thị hàm số \[y = f\left( x \right)\] trên hệ trục tọa độ \[{\rm{Oxy}}\].
b. Chứng minh rằng đồ thị hàm số đã cho luôn có hai giao điểm.
c. Gọi \[{{\rm{y}}_1};{y_2}\]là tung độ giao điểm của hai đồ thị. Tìm \[a\]để \[{{\rm{y}}_1} + {y_2} = 28\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
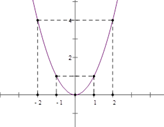
\(y = f\left( x \right) = {x^2}\) Bảng giá trị
Vẽ đồ thị như hình bên |
 |
||||||||||||
|
Phương trình hoành độ giao điểm của hai đồ thị \[{x^2} = 3ax - {a^2} \Leftrightarrow {x^2} - 3ax + {a^2} = 0\left( * \right)\] |
|||||||||||||
|
Ta có \[\Delta = {\left( {3a} \right)^2} - 4{a^2} = 5{a^2}\] |
|||||||||||||
|
Do \[\Delta > 0\] với mọi \[a \ne 0\], nên phương trình (*) luôn có hai nghiệm, hay đồ thị hai hàm số luôn có hai giao điểm. |
|||||||||||||
|
Gọi \[{x_1},{x_2}\] là hai nghiệm của phương trình (∗) ta được Và \[{x_1} + {x_2} = 3a;{x_1}{x_2} = {a^2}\]và |
|
\[{y_1} = 3a{x_1} - {a^2};{y_2} = 3a{x_2} - {a^2}\] \[{y_1} + {y_2} = 3a\left( {{x_1} + {x_2}} \right) - 2{a^2} = 9{a^2} - 2{a^2} = 7{a^2}\] (Hoặc \[{y_1} + {y_2} = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( {3a} \right)^2} - 2{a^2} = 7{a^2}\]) |
|
\[{y_1} + {y_2} = 28 \Leftrightarrow 7{a^2} = 28 \Leftrightarrow {a^2} = 4 \Leftrightarrow a = \pm 2\] Vậy \[a = \pm 2\] thỏa đề bài |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
\[{x^2} - 2mx + 2m - 3 = 0\] Với \[\]\[m = 0,5\] phương trình trở thành \[{x^2} - x - 2 = 0\] |
|
do \[a - b + c = 0\] nên phương trình có hai nghiệm \[{x_1} = - 1;{x_2} = - \frac{c}{a} = 2\]. |
|
Để phương trình \[{x^2} - 2mx + 2m - 3 = 0\] có hai nghiệm trái dấu thì \[a.c < 0\] |
|
\[ \Leftrightarrow 1.(2m - 3) < 0 \Leftrightarrow m < \frac{3}{2}\] |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Gọi \[x\] là số năm kể từ khi vào trường (\[x > 0\]). Chiều cao của cây bạch đàn theo số năm là \[y = \;x + 1{\rm{ }}(m)\] |
|
Chiều cao của cây phượng theo số năm là \[y = 0,5x + 3{\rm{ }}(m)\] |
|
Cây Bạch đàn cao hơn cây phượng khi \[x + 1 > 0,5x + 3\] |
|
\[ \Leftrightarrow 0,5x\; > 2 \Leftrightarrow x\; > 4\] Vậy sau 4 năm thì cây bạch đàn sẽ cao hơn cây phượng. |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập