Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 An Giang có đáp án
57 người thi tuần này 4.6 95 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
|
\[\frac{2}{{\sqrt 2 }}x + \sqrt 2 x = 4\] \[ \Leftrightarrow \frac{{2\sqrt 2 }}{2}x + \sqrt 2 x = 4\] \[ \Leftrightarrow \sqrt 2 x + \sqrt 2 x = 4\] |
\[\frac{2}{{\sqrt 2 }}x + \sqrt 2 x = 4\] \[ \Leftrightarrow \frac{{2\sqrt 2 }}{{\sqrt 2 }}x + 2x = 4\sqrt 2 \] \[ \Leftrightarrow 2x + 2x = 4\sqrt 2 \] |
|
\[ \Leftrightarrow 2\sqrt 2 x = 4\] \[ \Leftrightarrow x = \frac{4}{{2\sqrt 2 }}\] \[ \Leftrightarrow x = \sqrt 2 \] Vậy nghiệm của phương trình là \[x = \sqrt 2 \] |
\[ \Leftrightarrow 4x = 4\sqrt 2 \] \[ \Leftrightarrow x = \sqrt 2 \] Vậy nghiệm của phương trình là \[x = \sqrt 2 \] |
|
Giải phương trình \[{x^4} - 18{x^2} + 81 = 0\] Đặt \[t = {x^2}\] phương trình trở thành |
|
|
\[\begin{array}{l}{t^2} - 18t + 81 = 0\\\Delta ' = {9^2} - 81 = 0\end{array}\] |
|
|
Phương trình có nghiệm kép \[t = - \frac{{b'}}{a} = 9\] |
|
|
Với \[t = 9 \Rightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\] Vậy phương trình có hai nghiệm \[x = 3;x = - 3\] |
|
|
\(\left\{ \begin{array}{l}x + 3y = - 2\\2x - 4y = 16\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2x + 6y = - 4\\2x - 4y = 16\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x + 3y = - 2\\10y = - 20\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x + 3y = - 2\\y = - 2\end{array} \right.\) |
|
|
\( \Leftrightarrow \left\{ \begin{array}{l}x + 3\left( { - 2} \right) = - 2\\y = - 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = - 2\end{array} \right.\) Vậy hệ có nghiệm \(x = 4;y = - 2\) |
|
Lời giải
|
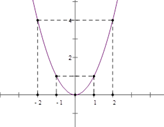
\(y = f\left( x \right) = {x^2}\) Bảng giá trị
Vẽ đồ thị như hình bên |
 |
||||||||||||
|
Phương trình hoành độ giao điểm của hai đồ thị \[{x^2} = 3ax - {a^2} \Leftrightarrow {x^2} - 3ax + {a^2} = 0\left( * \right)\] |
|||||||||||||
|
Ta có \[\Delta = {\left( {3a} \right)^2} - 4{a^2} = 5{a^2}\] |
|||||||||||||
|
Do \[\Delta > 0\] với mọi \[a \ne 0\], nên phương trình (*) luôn có hai nghiệm, hay đồ thị hai hàm số luôn có hai giao điểm. |
|||||||||||||
|
Gọi \[{x_1},{x_2}\] là hai nghiệm của phương trình (∗) ta được Và \[{x_1} + {x_2} = 3a;{x_1}{x_2} = {a^2}\]và |
|
\[{y_1} = 3a{x_1} - {a^2};{y_2} = 3a{x_2} - {a^2}\] \[{y_1} + {y_2} = 3a\left( {{x_1} + {x_2}} \right) - 2{a^2} = 9{a^2} - 2{a^2} = 7{a^2}\] (Hoặc \[{y_1} + {y_2} = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {\left( {3a} \right)^2} - 2{a^2} = 7{a^2}\]) |
|
\[{y_1} + {y_2} = 28 \Leftrightarrow 7{a^2} = 28 \Leftrightarrow {a^2} = 4 \Leftrightarrow a = \pm 2\] Vậy \[a = \pm 2\] thỏa đề bài |
Lời giải
|
\[{x^2} - 2mx + 2m - 3 = 0\] Với \[\]\[m = 0,5\] phương trình trở thành \[{x^2} - x - 2 = 0\] |
|
do \[a - b + c = 0\] nên phương trình có hai nghiệm \[{x_1} = - 1;{x_2} = - \frac{c}{a} = 2\]. |
|
Để phương trình \[{x^2} - 2mx + 2m - 3 = 0\] có hai nghiệm trái dấu thì \[a.c < 0\] |
|
\[ \Leftrightarrow 1.(2m - 3) < 0 \Leftrightarrow m < \frac{3}{2}\] |
Lời giải
|
Ta có \[\widehat {BAC} = 90^\circ \](góc nội tiếp chắn nửa đường tròn) |
![Cho tam giác \[ABC\left( {AB < AC} \right)\] nội tiếp trong đường tròn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid1-1766652226.png)
(hình vẽ cho câu a, 0,25đ) |
|
\[\widehat {BOD} = 90^\circ \](giả thiết) |
|
|
\[ \Rightarrow \widehat {BAC} + \widehat {BOD} = 180^\circ \]Vậy tứ giác nội tiếp |
|
|
Tam giác \[APO\] vuông tại \[A\], áp dụng định lý Pitago ta có \[P{O^2} = P{A^2} + O{A^2} \Rightarrow P{A^2} = P{O^2} - O{A^2}\] |
|
|
\[P{A^2} = {4^2} - {2^2} = 12\] \[PA = 2\sqrt 3 \,\,cm\] |
|
|
Mặt khác \[\tan \widehat {APO} = \frac{{OA}}{{AP}} = \frac{2}{{2\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\] |
|
|
\[ \Rightarrow \widehat {APO} = 30^\circ \] hay \[\widehat {APC} = 30^\circ \] |
|
|
Xét hai tam giác \[PBA\] và \[PAC\] có Góc \[P\] chung \[\widehat {PAB} = \widehat {PCA}\] (cùng chắn cung) Vậy hai tam giác \[PBA\] và \[PAC\] đồng dạng, khi đó \[\frac{{PB}}{{PA}} = \frac{{PA}}{{PC}} = \frac{{BA}}{{AC}}\] |
![Cho tam giác \[ABC\left( {AB < AC} \right)\] nội tiếp trong đường tròn (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid2-1766652251.png)
|
|
\[\frac{{PB}}{{PA}} = \frac{{BA}}{{AC}}\] và \[\frac{{PA}}{{PC}} = \frac{{BA}}{{AC}}\] Nhân hai biểu thức ta được \[\frac{{PB}}{{PA}}.\frac{{PA}}{{PC}} = \frac{{BA}}{{AC}}.\frac{{BA}}{{AC}} = {\left( {\frac{{BA}}{{AC}}} \right)^2}\]\[ \Leftrightarrow \frac{{PB}}{{PC}} = \frac{{B{A^2}}}{{A{C^2}}}\] |
|
Lời giải
|
Gọi \[x\] là số năm kể từ khi vào trường (\[x > 0\]). Chiều cao của cây bạch đàn theo số năm là \[y = \;x + 1{\rm{ }}(m)\] |
|
Chiều cao của cây phượng theo số năm là \[y = 0,5x + 3{\rm{ }}(m)\] |
|
Cây Bạch đàn cao hơn cây phượng khi \[x + 1 > 0,5x + 3\] |
|
\[ \Leftrightarrow 0,5x\; > 2 \Leftrightarrow x\; > 4\] Vậy sau 4 năm thì cây bạch đàn sẽ cao hơn cây phượng. |
